문제 : boj25418

필요 알고리즘 개념
- 동적계획법(DP), 너비 우선 탐색(BFS), 탐욕법(greedy)
- DP, BFS, 그리디 정도가 풀이로 생각나는 문제이다. 셋 다 알아야 하는건 아니고, 셋 중 하나만 알면 풀 수 있다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이 1 - DP 풀이
dp[x]를 x를 만들기 위한 최소 횟수로 정의하자. 그리고 dp[x]를 모두 무한대로(이 문제의 경우 나올 수 있는 최대수치가 100만이므로 100만1부터 무한대라고 생각하면 된다.) 초기화하고, dp[a] = 0으로 둔다.
이후 dp[a+1]부터 dp[k] 까지 이하의 점화식을 수행한 후, dp[k]를 출력해주면 된다.
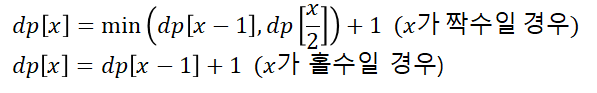
코드(DP) : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
int[] dp = new int[k+1];
Arrays.fill(dp, 1000001);
dp[a] = 0;
for (int i = a+1; i <= k; i++) {
dp[i] = dp[i-1];
if (i%2==0 && dp[i] > dp[i/2])
dp[i] = dp[i/2];
dp[i]++;
}
System.out.println(dp[k]);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}
풀이 2 - BFS 풀이
a부터 시작해서, a*2와 a+1로의 간선이 있는 탐색 문제로 생각하면 된다. 기본적인 형태의 bfs 구현이므로, 구현을 못하겠다면 일단 이 글을 먼저 보자. 이 때 당연히 방문 체크를 해야하긴 하나, a+1은 a*2보다 빠를 수 없으므로 a*2일 때만 방문했음을 체크하고, a+1일 때만 이미 방문했다면 진행 안해도 문제 없다(실제로 양쪽 다 방문체크한 것 보다 좀 더 빠르다 ㅋㅋ).
코드(BFS) : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
Queue<int[]> q = new ArrayDeque<>();
boolean[] v = new boolean[k+1];
q.add(new int[]{a,0});
v[a] = true;
while (!q.isEmpty()) {
int[] cur = q.poll();
if (cur[0] == k) {
System.out.println(cur[1]);
return;
}
if (cur[0]*2<=k) {
v[cur[0]*2] = true;
q.add(new int[]{cur[0]*2, cur[1]+1});
}
if (!v[cur[0]+1])
q.add(new int[]{cur[0]+1, cur[1]+1});
}
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}
풀이 3 - 그리디 풀이
당연히 +1보다는 x2를 해주는걸 더 많이 할수록 이득이라는 점은 누구든 알 수 있다. 하지만 a에서 k로 증가하면서는 적용해보려고하면, x2를 해주는 위치에 따라 답이 달라지므로 불가하다는걸 알아채고 bfs나 dp로 풀었을꺼다. 근데 반대로 생각해서 k에서 a로 내려오면서는 -1보다 /2를 더 많이 해주는 방식으로는 가능하다!
k부터 시작해서 짝수면 /2, 홀수면 -1을 해주면 된다.
코드(그리디) : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
int cnt = 0;
while (a!=k) {
cnt++;
if (k%2==0 && k/2>=a)
k/=2;
else
k--;
}
System.out.println(cnt);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| [자바, C++] 백준 2118 - 두 개의 탑 (java cpp) (2) | 2022.09.06 |
|---|---|
| [자바] 백준 1174 - 줄어드는 수 (java) (0) | 2022.09.05 |
| [자바] 백준 15232 - Rectangles (java) (0) | 2022.09.03 |
| [자바] 백준 1214 - 쿨한 물건 구매 (java) (2) | 2022.09.02 |
| [자바] 백준 25516 - 거리가 k이하인 트리 노드에서 사과 수확하기 (java) (0) | 2022.09.02 |





댓글