2022-07-21 업데이트 : 글 맨 아래에 '풀어보기'로 풀어볼만한 문제 링크 추가
2022-08-27 업데이트 : '풀어보기' 좀 더 추가, 목차 추가
목차
BFS (Breadth-first Search)
명확히 검증하면서 쓴게 아니라서 틀린 부분 있으면 알려주세요!
- BFS와 DFS

대충 곰처럼 생긴 섬이 바다에 떠 있다.
편의상 이 섬을 20등분해서 격자 형태로 구역을 나누었다.
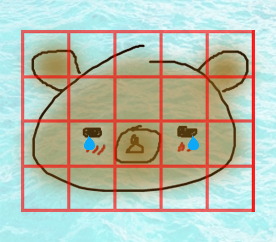
이제 우측상단의 귀(곰 입장에서 왼쪽귀)부터 출발해서 섬 전체를 둘러보려 한다.

둘러보는 방법은 여러가지가 있을 수 있다. 빨간 숫자는 둘러본 순서를 뜻한다. (0 부터 19까지)
- A처럼 자신과 가까운 곳부터 순서대로 살펴볼수도 있다. 격자형태로 나누었으므로 Manhattan Distance (Taxicab Geometry) 방식으로 거리를 쟀고, 해당 거리는 파란 글자로 나타냈음.
- B처럼 마이웨이를 외치며 그냥 내가 가는 곧이 곧 길이다! 를 외치며 그냥 한 길로 쭉 갈수도 있다. 여기선 외곽을 따라서 달팽이 모양으로 돌았다.
BFS는 항상 DFS와 세트로 생각하는 것이 좋다.
- 물에 돌멩이가 떨어졌을 때 생기는 동심원과 같이 시작점과 가까운 곳 부터 '차례대로' 살펴보면서 진행하는 것을 너비 우선 탐색 (BFS; Breadth-first search) 이라고 한다. (위 이미지의 A)
- 미로에서 일단 한 길을 선택해서 끝까지 가보고 (오른손법칙을 써도 마찬가지임) 막혀있다면 다시 이전 분기점으로 되돌아와 다른 길로 진행하는 것과 같이 거리와 상관없이 그냥 한 길로 '깊게' 마이웨이로 직진하는 것을 깊이 우선 탐색 (DFS; Depth-first Search) 라고 한다. (위 이미지의 B)
탐색이라는 개념에서 보자면 어쨌든 둘 다 모든 곳을 살펴볼 수 있으므로 뭘 쓰든 상관 없다. A와 B는 모두 0부터 19까지 살펴봤다.
하지만 BFS는 추가로 시작지점에서 가까운 곳부터 차례대로 방문했으므로, 시작점에서 각 지점까지의 거리도 알 수 있다. A에서 시작점 귀에서 다른 귀까지의 거리는 파란 숫자로 써둔 '4'이다.
- 그럼 무조건 BFS가 상위호환이 아닌가? 라는 생각이 들 수 있다. 일반적으로 맞다. DFS로 해결이 되는 경우라면 BFS로도 대부분 가능하다. 그 반대는 단순 탐색이 아닌 이상 성립하지 않는다.
- 다만, 미로에서 막힌 길을 만나면 그 이전 분기점까지 거슬러서 다시 돌아오면서 다시 안들어가게 길을 막아버리는 것(일종의 백트래킹) 처럼 DFS가 더 사용하기 좋은 경우도 있다. 또한 단순 탐색용 코드의 경우 DFS를 사용하는 것이 더 코드가 직관적이고 이해하기 쉽게 구성된다. 실제로 짜기도 DFS가 더 쉽다. BFS는 대부분 Queue를 사용해 구현하며, DFS는 Stack으로도 가능하지만 보통 재귀함수를 통해 많이 구현한다. (재귀함수는 처음에 이해하기가 어려워서 그렇지 일단 이해만 되면 코드가 직관적이고 간단해진다.)
- 위의 예시에서는 사실 DFS로도 거리를 알 수 있다. 단순히 시작점부터의 Manhattan Distance만 계산하면 된다. 하지만 중간중간 장애물이 있다면 그런식으로 계산을 할 수 없다.
- 배열 BFS
위의 곰 섬에서 해본게 배열에서의 BFS이다. 배열에서의 BFS는 알고리즘으로써 다양하게 쓰일 수 있다.
- 미로에서 탈출하기 위한 최단 경로의 길이 구하기 (BFS 특성을 통해 배열형태로 구성된 미로를 탐색하며 최단거리 탐색)
- 현재 떨어지고 있는 테트리스 조각이 딱 맞게 들어갈 공간이 있는지 (탐색을 통해 현재 떨어지는 블록의 모양과, 이미 만들어둔 블록의 모양 확인)
- 체스판 상태가 주어질 때 왕이 안움직인다면 나이트가 왕을 잡도록 최소 몇 번만에 움직일 수 있는지 (이후 설명할테지만, 배열에서 BFS는 반드시 상하좌우로 인접한 위치로 이동하지 않아도 된다. 나이트의 이동처럼 독특한 방식으로 이동해도 가능하다.)
- 등
0. 아래와 같은 미로가 있다. 한 번 같이 BFS를 사용해 미로를 탈출하는 가장 빠른 거리를 찾아보자. 이 때, 미로 외곽은 모두 장애물이라 가정하며, 이동은 상하좌우로 인접한 칸으로 이동할 수 있다. 즉, 대각선으로 이동은 불가하다. [ 'S' : 시작점, '숫자' : 이동 가능한 곳, 'X' 장애물 ] 을 나타낸다. 또한 각 인접한 칸 사이의 거리는 모두 동일한 '1'이라 가정한다.

- BFS는 일반적으로 Queue 자료구조를 사용해 진행한다. FIFO(First in first out)의 특성을 가진 자료구조로 시작점에서 부터 단순히 인접한 이동 가능한 위치들을 큐에 넣으며 탐색을 하면 그게 결국 BFS가 된다. 이하 과정을 보면 이해될 것 이다. 이하 미로 아래의 배열은 Queue를 뜻한다. 좌측으로 넣고, 우측으로 빼낸다고 가정한다.
1. 우선 시작점인 S를 큐에 넣는다. 이 때 거리도 재야 하므로, 괄호내의 숫자는 거리를 뜻한다. 만약 거리가 필요없고, 단순히 탐색만 필요하다면 괄호 부분은 없어도 된다. 이미 방문한 곳은 빨간색으로 표시했다.

- 시작점이므로 거리는 0이다.
2. 큐에서 하나를 빼보니 S(0)이다. 그럼 빼낸 칸과 인접해있고 이동 가능한 모든 칸인 1과 4를 큐에 넣는다. 이 때 거리는 큐에서 빼낸 칸의 거리+1 이다. 이 때, 인접한 곳 끼리는 우선순위가 없다. 따라서 1을 먼저 넣던지 4를 먼저 넣던지 상관 없다.

3. 다시 큐에서 하나를 빼보니 1(1)이다. 마찬가지로 인접한 칸인 2을 큐에 넣는다. 역시 거리는 현재 큐에서 뺀 칸에 기록된 거리+1 이다.
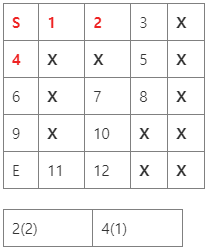
4. 이번에 빼보니 4(1)이다. 6을 큐에 넣는다.

5. 이번엔 2(2)이다. 3을 넣는다. 마찬가지로 거리는 (2+1)이 된다.

6. 이번엔 6(2)이므로 역시 9(3)을 큐에 넣는다.

7. 다시 큐에서 뺀게 3(3)이므로 인접한 5(4)를 넣는다.

8. 이번엔 9(3)이 빠지게 되고, 인접한 곳이 최종 목적지인 E 이다!
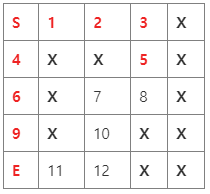
- 큐가 사라졌다! 왜냐면 목적지까지의 최단거리만 알면 되므로, 더이상 진행해볼 필요가 없다. 최종적으로 E(4)로 프로그램은 종료된다. S에서 E까지의 최단거리는 4라는 점을 알 수 있었고, 전체를 탐색할 필요도 없이 완료하게 되었다.
위의 과정을 자바 코드로 구현해보겠다. 입력은 콘솔입력으로 다음과 같이 넣는 것을 가정하겠다. 칸 번호는 설명의 편의를 위해 넣은 것이므로 이하 입력과 같이 이동할 수 있는 곳은 'O'로 넣도록 하겠다. 첫 줄의 '5 5'는 이하 입력될 배열의 row 수 'R', column 수 'C'를 의미한다. 2번째 줄부터 R+1 줄까지 배열의 각 row를 입력 받아야 하며, 각 줄은 C개의 char를 포함한다. 출력은 콘솔출력으로 S에서 E까지의 최단거리를 출력한다. 이 때, 발견하지 못한다면 -1을 출력한다.
5 5
SOOOX
OXXOX
OXOOX
OXOXX
EOOXX
짜본 코드는 다음과 같다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static class Pos {
int r, c, dist;
public Pos(int r, int c, int dist) {
this.r = r;
this.c = c;
this.dist = dist;
}
}
private static final int[] DR = {1, 0, -1, 0};
private static final int[] DC = {0, 1, 0, -1};
private static final char MAZE_START = 'S';
private static final char MAZE_BLOCK = 'X';
private static final char MAZE_END = 'E';
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
final int R = Integer.parseInt(st.nextToken());
final int C = Integer.parseInt(st.nextToken());
Queue<Pos> q = new LinkedList<>(); // BFS를 위한 큐
boolean[][] visited = new boolean[R][C]; // 이미 방문한 곳을 다시 가지 않도록 방문체크
// 미로 입력 받기
char[][] maze = new char[R][C]; // 미로맵을 받아둘 배열
for (int i = 0; i < R; i++) {
String curRow = br.readLine();
for (int j = 0; j < C; j++) {
char curCol = curRow.charAt(j);
if (curCol == MAZE_START) {
q.add(new Pos(i, j, 0)); // 시작위치를 발견하면 바로 큐에 넣음
visited[i][j] = true; // 시작위치를 큐에 넣었으므로 방문한 것으로 체크
}
maze[i][j] = curRow.charAt(j);
}
}
// BFS 진행
while (!q.isEmpty()) {
Pos cur = q.poll(); // 큐에서 하나를 뽑아냄
for (int i = 0; i < DR.length; i++) { // 인접한 칸으로 탐색 진행
int nextR = cur.r + DR[i];
int nextC = cur.c + DC[i];
int nextDist = cur.dist + 1;
if (nextR < 0 || nextR >= R || nextC < 0 || nextC >= C || visited[nextR][nextC] || maze[nextR][nextC] == MAZE_BLOCK) {
continue; // 다음 탬색할 위치가 미로를 벗어난 위치이거나 이미 방문한 곳이거나 장애물인 경우 탐색에서 제외
}
if (maze[nextR][nextC] == MAZE_END) { // 최종 목적지를 발견한 경우
System.out.println(nextDist); // 거리를 출력하고,
return; // 그대로 종료하면 됨.
}
q.add(new Pos(nextR, nextC, nextDist)); // 큐에 다음 탐색할 곳을 넣음.
visited[nextR][nextC] = true; // 큐에 넣은 곳 방문체크
}
}
System.out.println(-1); // 발견을 하지 못한 예외의 경우 -1을 출력.
}
}
위에서 그림으로 설명했던 내용을 코드로 구현하면 된다. 인접한 칸은 상하좌우로 인접한 칸이므로, DR과 DC를 동일한 index끼리 묶어보면 "(1, 0) : row+1이므로 배열에서 아래로 한칸 내려감 / (0, 1) : column+1이므로 배열에서 오른쪽으로 한 칸 이동함 / (-1, 0) : 마찬가지로 배열에서 위로 한칸 이동함 / (0, -1) : 마찬가지로 배열에서 좌측으로 이동함." 이 된다.
TMI로, 일반적으로 사용하는 Scanner를 통한 입력은 항상 regex를 검색하므로 느리다. BufferedReader를 통한 입력이 훨씬 더 빠르며, CP(경쟁 프로그래밍)에서는 그것도 느리다고 판단해서 보통 개개인마다 자신만의 입출력 코드를 미리 만들어두고 사용한다. 마찬가지로 String에 대한 split() 보다 StringTokenizer가 더 빠르다. 기타 BFS에 대한 설명은 주석에 달아두었다.
- 방문체크!
여기까지 설명을보면서 뭔가 이상한 점을 하나 발견할 수 있다. 그림을 가지고 설명할 때는 별 생각을 못했겠지만, 사실 BFS나 DFS에서는 방문체크가 반드시 필요하다. 코드에서는 boolean[][] visited 로 나타난다. 머리속으로 생각할 때는 이미 왔던 곳이니 당연하게 배제하고 생각했겠지만, 프로그램은 안짜주면 그런거 모른다. 위에서 표로 설명하던 부분에서 '3'번 과정을 보자. 1(1)을 큐에서 빼고 2(2)를 넣었었다. 여기서 코드에 있는 visited 배열같은게 없다면 사실 S(2)도 큐에 집어넣게된다. 인접해있으니까 당연하다. 그리고 그렇게 무한루프에 빠지게 될 위험이 있고, 빠지지 않더라도 메모리와 시간복잡도 모두 엄청나게 손해를 보게된다. 그러니 BFS와 DFS에서는 항상 방문체크가 필요함을 잊으면 안됨.
- 배열에서 상하좌우로 인접한 경우에만 BFS가 가능할까?
그렇지 않다. 나이트의 이동을 예시로 들어보겠다. 우선, 체스에서 나이트는 아래와 같이 이동 가능하다.

그럼 이걸 코드로 옮겨보겠다. 제시된 조건은 위와 동일하며, 이동만 상하좌우가 아니라 나이트가 이동하는 방식으로 변경한 것이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static class Pos {
int r, c, dist;
public Pos(int r, int c, int dist) {
this.r = r;
this.c = c;
this.dist = dist;
}
}
private static final int[] DR = {-1, -2, -2, -1, 1, 2, 2, 1};
private static final int[] DC = {-2, -1, 1, 2, 2, 1, -1, -2};
private static final char KNIGHT_START = 'S';
private static final char KNIGHT_BLOCK = 'X';
private static final char KNIGHT_END = 'E';
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
final int R = Integer.parseInt(st.nextToken());
final int C = Integer.parseInt(st.nextToken());
Queue<Pos> q = new LinkedList<>(); // BFS를 위한 큐
boolean[][] visited = new boolean[R][C]; // 이미 방문한 곳을 다시 가지 않도록 방문체크
// 체스판 입력 받기
char[][] chess = new char[R][C]; // 체스판을 받아둘 배열
for (int i = 0; i < R; i++) {
String curRow = br.readLine();
for (int j = 0; j < C; j++) {
char curCol = curRow.charAt(j);
if (curCol == KNIGHT_START) {
q.add(new Pos(i, j, 0)); // 시작위치를 발견하면 바로 큐에 넣음
visited[i][j] = true; // 시작위치를 큐에 넣었으므로 방문한 것으로 체크
}
chess[i][j] = curRow.charAt(j);
}
}
// BFS 진행
while (!q.isEmpty()) {
Pos cur = q.poll(); // 큐에서 하나를 뽑아냄
for (int i = 0; i < DR.length; i++) { // 인접한 칸으로 탐색 진행
int nextR = cur.r + DR[i];
int nextC = cur.c + DC[i];
int nextDist = cur.dist + 1;
if (nextR < 0 || nextR >= R || nextC < 0 || nextC >= C || visited[nextR][nextC] || chess[nextR][nextC] == KNIGHT_BLOCK) {
continue; // 다음 탬색할 위치가 체스판을 벗어난 위치이거나 이미 방문한 곳이거나 장애물인 경우 탐색에서 제외
}
if (chess[nextR][nextC] == KNIGHT_END) { // 최종 목적지를 발견한 경우
System.out.println(nextDist); // 거리를 출력하고,
return; // 그대로 종료하면 됨.
}
q.add(new Pos(nextR, nextC, nextDist)); // 큐에 다음 탐색할 곳을 넣음.
visited[nextR][nextC] = true; // 큐에 넣은 곳 방문체크
}
}
System.out.println(-1); // 발견을 하지 못한 예외의 경우 -1을 출력.
}
}
이전 배열 BFS 코드를 봤다면 거의 변경되지 않았음을 알 수 있다.
사실 바뀐 부분은 DR과 DC를 나이트의 이동 방식에 맞게 변경했을 뿐이다. (그 외에는 단순히 변수명변경, 주석 변경)
- 그래프 BFS
이제 배열에서 BFS 하는 방법에 대해서는 어느정도 파악했을 것이다. 그럼 이번엔 그래프로 가보자. 배열에서의 BFS가 이해됬다면 그래프도 쉽다.
0. 우선 다음과 같은 그래프가 있다. 1번에서 출발해서 마지막 번호 (6번)까지 가려 한다. 모든 간선은 이동하는데 동일한 가중치(1로 가정한다)가 필요하다고 하자. 또한 무방향 그래프이다. (양방향으로 이동 가능)

1. 시작점인 1을 큐에 넣는다. 배열 BFS와 마찬가지로 큐에 기입된 1(0)은 '노드번호(거리)'를 의미한다.
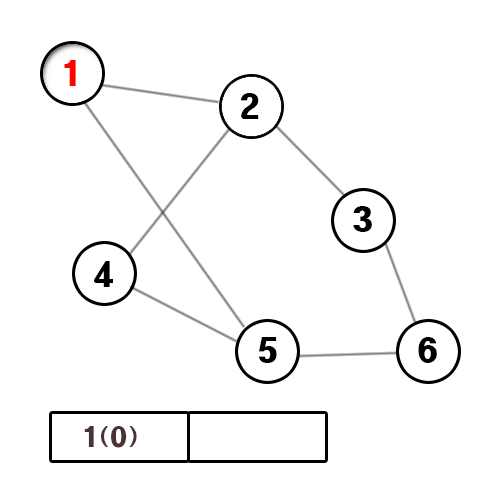
2. 큐에서 하나를 뺀다. 1(0)이므로 간선(edge)이 연결된 곳을 모두 큐에 넣는다. 마찬가지로 거리는 현재 거리에서 1을 더해서 넣어준다.

3. 역시 큐에서 하나를 뺀다. 2(1) 이므로 인접한 3(1+1)와 4(1+1)를 넣어준다.
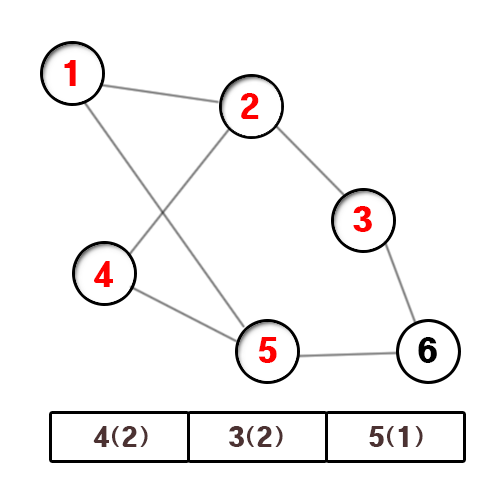
4. 다음으로 5(1)을 큐에서 빼고 보니 인접한 곳이 목적지인 6(1+1) 이다. 큐에 남아있던건 더이상 필요없다. 목적지를 찾았고, 거리는 2임을 알 수 있다.

마찬가지로 위에서 설명한 그래프에서의 BFS를 코드로 구현해보겠다.
입력은 아래와 같은 방식으로 콘솔입력으로 주어진다고 가정한다. 첫번째 줄에 정점(vertex)의 갯수 N이 주어진다. 아래의 입력 예시에서는 '6'이므로 1~6까지 6개의 정점이 있음을 나타낸다. 두번째 줄에 간선(edge)의 갯수 E가 주어진다. 아래에서는 '7'이므로 이후 7줄에 걸쳐 간선 정보가 주어질 것이다. 그 다음줄부터 간선 갯수만큼 간선 정보가 주어지며, 양방향 간선이다.
6
7
1 2
1 5
2 4
2 3
3 6
4 5
5 6출력으로는 1번부터 마지막 정점까지의 최단거리를 출력하면 된다. 만약 주어지는 간선들로는 마지막 정점까지 갈 수 없을 경우 -1을 출력한다.
우선 기본적인 방식으로 인접 행렬을 통해 그래프의 간선을 표현해서 짜본 코드이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int e = Integer.parseInt(br.readLine());
// 간선정보 입력받기
boolean[][] edge = new boolean[n+1][n+1]; // 간선 정보 저장
while (e-- > 0) {
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
edge[a][b] = true;
edge[b][a] = true; // 양방향 간선이므로 반대방향도 넣어줘야 함.
}
// BFS 진행
Queue<Integer> q = new LinkedList<>(); // BFS를 위한 큐
boolean[] visited = new boolean[n+1]; // 방문체크
int[] dist = new int[n+1]; // 거리정보
Arrays.fill(dist, -1);
q.add(1);
visited[1] = true;
dist[1] = 0;
while (!q.isEmpty()) {
int cur = q.poll();
for (int i = 1; i <= n; i++) {
if (!edge[cur][i] || visited[i]) {
continue; // 간선정보가 없는 위치거나 이미 방문했다면 무시
}
int next = i;
q.add(next); // 다음 간선 번호를 큐에 넣음
visited[next] = true; // 방문체크
dist[next] = dist[cur] + 1; // 거리 정보
if (i == n) {
break; // 목적지에 도달했다면 break로 나감. 배열 BFS 예시처럼 출력하고 return해도 동일함.
}
}
}
System.out.println(dist[n]); // 방문한적 없다면 위에서 Arrays.fill로 -1로 초기화했으므로 -1이 출력될 것임.
}
}
- 다양한 방식의 예시를 들기 위해 이번엔 클래스로 정의하지 않고 단순히 간선 번호인 Integer를 넣는 큐를 구성해봤다. 이 때 거리정보를 넣을 수 없으므로 따로 dist 배열을 둬서 거리정보를 넣도록 했다. 배열 BFS에서도 때에 따라 더 빠른 방식으로 BFS를 돌려야할 경우 클래스를 쓰지 않고 큐 2개에 각각 row, column 값을 넣어서 짜기도 한다. 배열 BFS와 원리상에서 차이가 아예 없음을 알 수 있다.
- 배열 선언 시 크기가 n+1 로 한 것은, 위 예시에서 정점 번호가 1번부터 6번까지이기 때문이다. 배열을 6개짜리를 만들면 인덱스 0부터 5를 써야하는데, 그럼 edge를 입력받을 때 입력으로 제시된 정점 번호를 모두 -1해서 받아야 한다. 이럴 땐 그냥 배열의 0번 인덱스 부분의 메모리를 버린다고 생각하고 그냥 배열 크기를 1개 늘려서 생성하면 편하다.
다음으로 위 코드를 기반으로 인접 리스트를 사용해 간선을 표현해서 BFS를 돌려보겠다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int e = Integer.parseInt(br.readLine());
// 간선정보 입력받기
ArrayList<Integer>[] edge = new ArrayList[n+1]; // 간선 정보 저장
for (int i = 1; i <= n; i++) {
edge[i] = new ArrayList<>();
}
while (e-- > 0) {
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
edge[a].add(b);
edge[b].add(a); // 양방향 간선이므로 반대방향도 넣어줘야 함.
}
// BFS 진행
Queue<Integer> q = new LinkedList<>(); // BFS를 위한 큐
boolean[] visited = new boolean[n+1]; // 방문체크
int[] dist = new int[n+1]; // 거리정보
Arrays.fill(dist, -1);
q.add(1);
visited[1] = true;
dist[1] = 0;
while (!q.isEmpty()) {
int cur = q.poll();
for (int next : edge[cur]) {
if (visited[next]) {
continue; // 이미 방문했다면 무시
}
q.add(next); // 다음 간선 번호를 큐에 넣음
visited[next] = true; // 방문체크
dist[next] = dist[cur] + 1; // 거리 정보
if (next == n) {
break; // 목적지에 도달했다면 break로 나감. 배열 BFS 예시처럼 출력하고 return해도 동일함.
}
}
}
System.out.println(dist[n]); // 방문한적 없다면 위에서 Arrays.fill로 -1로 초기화했으므로 -1이 출력될 것임.
}
}
위 인접 행렬로 짠 코드에서 edge를 저장하는 배열만 변경되었고, 수행하는 일은 동일하다. 주의점은 ArrayList의 배열이므로 참조형 배열이다. 참조형의 배열에는 Arrays.fill 함수를 통해 Arrays.fill(edge, new ArrayList<>()); 를 수행하게 되면 모든 배열에 하나의 동일한 ArrayList를 참조하게 된다. 이처럼 참조형 배열에는 Arrays.fill 함수를 사용하면 안되고 반복문을 돌려서 하나씩 초기화해줘야 한다.
- 사실 배열 BFS도 그래프 BFS와 동일하다.

배열 A에서 상하좌우로 인접한 칸에 대한 BFS는 그래프 B와 동일하다. 그러니 원리만 알았다면 배열이던 그래프이던 상관이 없다.
TMI : 배열로 처리하기 복잡한 경우 배열을 그래프로 변경해서 풀기도 한다. 나중에 다루겠지만 예를들어 flood fill 알고리즘을 적용한 후 각 그룹에 대한 연산은 그래프로 만들어서 돌리는 등의 방법이 자주 쓰인다.
예를들어 다음과 같은 배열이 있다.

여기에서 번호가 같은 곳 끼리는 시간의 소모 없이 움직일 수 있고, 번호가 다를 때만 이동하는데 가중치가 든다고 해보자. 이러한 경우 물론 배열 BFS로도 해결은 할 수 있다. 하지만 배열의 크기가 엄청나게 클 경우 BFS로는 매우 비효율적이다. 그럼 일단 DFS나 BFS를 통해 같은 번호를 탐색하고, 탐색할 때 마다 인접한 곳의 번호를 기록해둔다면 위 배열은 아래와 같은 그래프로 간단하게 나타낼 수 있게 된다.
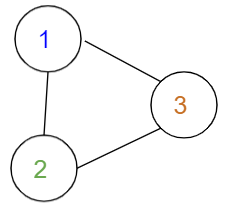
전처리를 통해 정점 3개인 그래프로 변경이 되었다. 이에 대한 BFS는 위 배열에서 그대로 BFS를 돌린 것 보다 시간복잡도 면에서 매우 효율적일 것임을 짐작할 수 있다.
- BFS 시간 복잡도를 살펴보자.
- 우선 처음에 봤던 배열 BFS를 보자. 최악의 경우 모든 칸을 봐야 하고, 각 칸마다 인접한 칸을 최대 4개 봤다. row의 갯수를 R, column의 갯수가 C일 때 모든 칸의 갯수는 R * C 이며, 이걸 N이라고 하자. 그럼 최종적으로 [N칸을 탐색 + 각 칸마다 4개의 인접한 칸을 봄] = O(N + 4N) = O(N) = O(R*C)가 된다.
- 다음으로 그래프 BFS 중 인접 행렬을 사용한 경우를 보자. 모든 정점의 갯수를 V라 하고, 모든 간선의 갯수를 E라 하자. 그런데 인접 행렬의 경우 간선의 갯수와 상관없이 모든 간선 쌍에 대해 연결여부를 인접 행렬로 표현한 것이기 때문에 간선의 갯수와 상관없이 V^2개의 간선 정보를 확인해야 한다. 따라서 [모든 정점을 확인했고 + 가능한 모든 간선쌍을 확인함] = O(V + V^2) = O(V^2)이 된다.
- 마지막으로 그래프 BFS 중 인접 리스트를 사용한 경우이다. 모든 정점의 갯수를 V라 하고, 모든 간선의 갯수를 E라 하자. 이건 간단하게 [모든 정점 확인 + 모든 간선 확인] = O(V+E) 가 된다.
- 그런데 왜 인접한 곳 사이의 거리가 전부 1임?
지금까지 살펴본 모든 예시들은 신기하게도 인접한 경우 거리가 1이었다. 사실 최단 거리를 구하기 위한 알고리즘은 BFS 말고도 많이 있다. '0-1 BFS' 같은 다른 방식도 있긴하지만, 일반적인 BFS의 경우 최단 거리 찾기 분야(?)에서 가중치가 모두 동일한 경우만을 담당한다.(반드시 가중치가 1일 필요는 없다. 모두 동일하다면 1로 치고 연산하고 최종 출력 때 곱하면 된다.)
차차 다루겠지만 간략히 다른 길찾기 알고리즘에 대해 써보면 다음과 같다.
- BFS : 가중치가 동일할때만 길을 찾을 수 있다.
- Dijkstra : 가중치가 양의 정수일 때 가능. 네비게이션에서 쓰임
- Floyd-Washall : 모든 정점에서 모든 정점으로의 최단거리를 한방에 구할 수 있다. 다만 시간복잡도가 O(N^3)이다.
- Kruskal, Prim: 가중치가 음이어도 가능하다.(음의 사이클이 있으면 안됨)
- 방문체크에 대해 좀 더 써봄
미로에 대한 BFS를 진행했던 '배열 BFS' 부분에서 좀 더 생각해보자.
결국 방문체크(방문배열)란 것은, BFS에서 '모든 경우'를 살펴보며 진행할 때, 같은 행위를 두번하면 비효율적이니 그걸 막기 위해 사용한다. 따라서 방문배열은 BFS를 진행할 때 탐색할 수 있는 '모든 경우'를 나타낼 수 있어야 한다. 일반적인 BFS 탐색 문제에서 모든 경우는 결국 '이 위치에 이미 왔었다'면 된다. 따라서 위 미로 예시에서는 단순히 2차원 방문배열로 나타내면 됬다.
그럼 좀 더 확장해서 생각해보자. 위 미로 문제에서 장애물('X' 부분)을 한 번까지는 부수고 이동할 수 있다고 하자. 그럼 '모든 경우'가 변한다. 말로 하자면 '해당 위치에 장애물을 부순 상태로 이미 왔었거나, 해당 위치에 아직 장애물을 부수지 않은 상태로 이미 왔었다.'가 된다. 이걸 표현하려면 방문배열이 다음과 같이 변경되야 한다. boolean[][][] visited. 여기서 1차와 2차는 동일하고, 3차는 0일 경우 아직 장애물을 부수지 않은 경우, 1일 경우 장애물을 부순 경우에 대해 체크하면 된다. 예를들어 visited[0][0][0]은 처음 시작하는 S의 위치이다. 이후 아래로 장애물을 부수며 한 번 내려갔다. 원래대로면 다시 S 지점으로 못돌아와야하지만 여기서는 장애물을 부쉈는지도 체크하기 때문에 되돌아올 수 있으며 visited[0][0][1]이 체크 되게 된다. 그럼 이렇게 하지 않을 경우 어떻게 되는지 생각해보자.
SOOOOO
XXXXXO
OXOOOO
OXOXXX
OXOOXX
OXXOXX
OOO*XE미로가 다음과 같이 생겼다고 하자. 장애물은 1번은 깨고 진행할 수 있다. 이 때 방문배열을 기존과 똑같이 2차원 배열로 사용했다.
S지점에서 아래쪽으로 장애물을 뚫고 진행한 녀석은 *까지 빠르게 갈것이다. 이 때 *도 O인데 설명하려고 *이라고 해뒀다. 어쨌든 *까지 도달했으니 *에도 방문배열에 체크를 했다. 이미 장애물을 뚫고 진행했으니 목적지에는 도달할 수 없다.
그 와중에 S지점에서 오른쪽으로 진행한 녀석은 꼬불꼬불한 길을 따라 천천히 * 직전까지 온다. 사실 얘는 *까지만 오면 장애물을 아직 안부셨으니깐 목적지(E) 좌측의 장애물을 부수고 목적지에 갈 수 있다. 하지만 이미 방문체크가 되어있으니 * 지점에 갈수가 없고, 따라서 프로그램은 목적지에 도달하지 못한다고 판단하고 -1을 출력하게 된다. 이런식으로 모든 경우를 나타낼 수 있는 방문배열을 만들지 않을 경우 문제가 생기게 된다.
풀어보기
코드, 코드 및 해설은 풀다가 정 모르면 보시는걸 추천드립니다. 푼지 오래된 문제의 경우 제 코드가 다소 비효율적일 수 있습니다.
1. 백준 24444 : 알고리즘 수업 - 너비 우선 탐색 1 (코드 및 해설)
-> 기본적인 형태의 bfs 알고리즘 문제
-> bfs 탐색을 통해 구역의 수를 세는 문제. 출발 지점이 딱히 정해져 있지 않은 상태에서 bfs를 진행하는 연습!
-> 이번엔 bfs를 진행하는 곳이 2차원이 아님. 3차원에서 bfs 해보기!
-> 상하좌우로 인접한 곳만 가지 않고, 독특한 방법으로 움직일 때 bfs 진행해보기!
5. 백준 24513 : 좀비바이러스 (코드 및 해설)
-> 요정도 한다면 방문배열을 독특하게 설정해야하는 문제가 아닌 단순 탐색 형태의 bfs 문제는 앞으로 문제 없을 것임.
-> 글에서 '방문체크에 대해 좀 더 써봄'을 쓰게된 계기가 된 문제
7. 백준 14442 : 벽 부수고 이동하기 2 (코드)
-> '6'에서 좀 더 진화함! 개념은 동일함.
-> 요정도 한다면 방문체크로 고생할 일도 앞으로 거의 없을것임.
-> 요정도 한다면 뭐 코테수준에서 bfs로 문제생길일은 없을 것임
10. AtCoder Beginner Contest 259 - D : Circumferences (코드 및 해설)
-> 이런식으로도 사용할 수 있구나 정도로 한번 해보면 좋음.
11. 백준 22949 - 회전 미로 탐색 (코드 및 해설)
-> 완전 강추. 이 글을 이해했다면 풀 수 있다. 요 정도 풀면 순수 BFS 문제에서는 문제될 일 없을 것 같다.
'CS > Algorithms' 카테고리의 다른 글
| 누적 합(prefix sum), 2차원 누적합(prefix sum of matrix) with java (11) | 2022.08.09 |
|---|---|
| 분할 정복을 이용한 거듭제곱 최적화 (0) | 2022.04.05 |
| 에라토스테네스의 체 혹은 소수판정 시 제곱근 까지만 확인하면 되는 이유 (4) | 2022.02.12 |
| 백트래킹 알고리즘 (Back Tracking) (0) | 2021.10.03 |
| 알고리즘 시간복잡도에 대해 (0) | 2021.09.22 |





댓글