문제 : boj1017
애초에 해결을 위한 키 아이디어도 일반적으로 찾기 쉽지 않을듯하고, 거기에 네트워크 플로우에서 이분 그래프의 최대 유량을 구하는 이분매칭 알고리즘에다가 소수 판정(에라토스테네스의 체)에다가 값 압축(이건 필수는 아님)까지 들어간 플래3에 손색이 없는 문제였다. 구현이 다소 복잡했어서 틀리면 예외찾을 엄두가 안났었는데 다행히 운좋게 한방에 통과했다. 오랜만에 한방에 통과한게 찐텐으로 기뻤다ㅋㅋ

1.
일단 브루트포스로 모든 경우를 살펴본다면 50C2번에 걸쳐 더해서 소수쌍이 되는걸 구하고, 모든 소수가 되는 쌍에 대해 모든 N개가 서로 겹치지 않고 선택되는 경우를 살펴야 한다. 대강 모든 쌍의 합이 소수가 된다면 O((50C2)!) 정도가 될 것이므로 통과할 수 없다.
서로 최대한 쌍을 만드는 이런 경우에 이분매칭 개념을 알고 있다면 이분매칭으로 접근해볼 수 있다. 하지만 문제에서 제시된 그대로는 이분매칭 개념을 적용할 수 없다. 일단 이분 그래프를 만들어야 한다. 여기에 '키 아이디어'가 필요한데, 이 문제의 경우 1000보다 작거나 같은 자연수이고 서로 중복되지 않으므로 두 수의 합이 '2'가 되는 경우는 없다. 따라서 모든 소수는 짝수+홀수의 합으로 만들어질 수 있을 것이다. 따라서 짝수 정점과 홀수 정점으로 나누면 이분 그래프를 만들 수 있다.
'예제 입력 4'를 보자. (이후 모든 설명은 이걸 가지고 진행한다.)
8
34 39 32 4 9 35 14 17
에 대해 우선 홀수와 짝수로 나눠 보겠다.
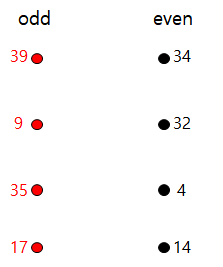
'1'의 내용은 코드의 'separate even and odd numbers' 부분에 해당한다. 또한 여기서 홀수의 개수와 짝수의 개수가 다르다면 모든 쌍을 매칭하는 경우가 존재할 수 없으므로 -1을 출력하고 종료하면 된다. (예외1 - 코드 82 line)
2.
이 문제에서 중심이 되는 것은 '첫 번째 수와 어떤 수를 짝지었는지' 이다. 물론 첫 번째 수와 합쳐져 소수가 가능한 모든 값에 대해 고정시키고 매번 이분매칭을 진행할 수도 있으나 비효율적이다. 첫 번째 수를 제외한 나머지 값들에 대해 이분매칭을 진행한 후, 첫 번째 수와 합쳐져 소수가 되는 모든 값에 대해 매칭이 가능한지 보는 것이 훨씬 효율적이다.
따라서 개념적으로 좌측에서 우측으로 매칭을 진행한다고 한다면, 첫 번째 수가 홀수라면 홀수가 좌측, 짝수가 우측에 오도록 해야 한다. 짝수라면 좌측이 짝수, 우측이 짝수가 된다. 예제 입력 4에서는 첫 번째 수가 짝수이므로, 위에서 그렸던 이미지를 재배치한다.

'2'의 내용은 코드의 'choice left side and right side' 에 해당한다.
3.
이제 이분 그래프를 만들 정점들이 마련되었으니 간선을 만들어야 한다. 두 수의 합이 소수가 된다면 간선이 존재하는 경우이다. 두 수 합의 최대치는 약 2000이므로(각 값은 1000이하의 자연수이므로) 2000까지의 모든 소수를 우선 구한다(코드의 findPn). 그리고 left - right의 모든 쌍에 대해 합이 소수인지 확인하여 간선을 만든다(코드의 findEdge).
'예제 입력 4'의 경우 다음과 같은 간선이 만들어진다. 예를들어 34+35인 69는 소수가 아니다. 34+39와 34+9는 소수이다.

이 때, 만약 left에서 right로의 간선이 하나도 만들어지지 않은 정점이 존재한다면 볼 것도 없이 모든 쌍에 대한 매칭이 불가하므로 -1을 출력하고 종료하면 된다. (예외 2 - 코드 95 line)
추가로 이대로 진행한다면 값을 기준으로 매칭을 진행해야 하므로 1000개짜리 배열이 필요하다. 값은 1000까지이지만, N은 최대 50개이고 짝수와 홀수의 개수가 같아야하므로 최대 25개로 값을 압축시킬 수 있다. 압축한 결과는 다음과 같다. idx가 압축된 값이고, 배열값이 실제 값이다. 코드에서는 findEdge를 하면서 압축된 값을 기준으로 진행했다. 이후 설명은 실제 값을 기준으로 한다.
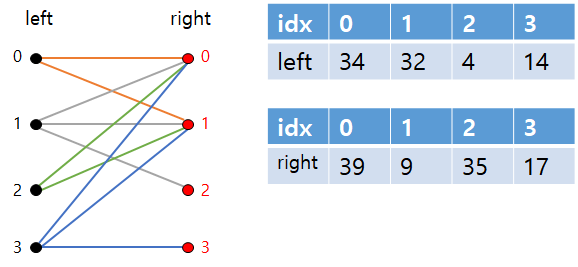
4.
이제 처음으로 나왔던 수(left 최상단)가 가진 2개의 간선을 하나씩 고정시킨 후 이분매칭으로 전체를 매번 살펴도 답을 구할 수 있다. 이렇게 해도 통과 가능하다.
하지만 좀 더 효율적으로 진행해보기 위해 우선 처음 입력된 수를 제외한 나머지에 대해 이분매칭을 진행한다(즉, left에서 최상단을 제외한 나머지에 대해 먼저 진행). 이 때 첫 입력값을 제외한 나머지에 대해서 매칭이 불가한 정점이 있다면 -1을 출력하고 종료한다. (예외 3 - 코드 107 line)
결과는 다음과 같다. 모양은 구현방식에 따라 다를 수 있다. 이 부분이 코드의 'bipartite matching'에 해당한다.

5.
마지막으로 첫 번째로 입력된 수의 각 간선을 '4'의 결과에 끼워넣어 매칭이 가능한지 확인한다. 가능한 간선이라면 List에 넣어둔다. 바로 출력하지 않는 이유는 '오름차순'으로 출력하라고 했기 때문에 정렬이 필요하기 때문이다.
위의 경우에서 34->39 로의 간선을 연결한 경우를 보자. 14->39 간선을 치워야 한다. 14->17로 치우면 바로 가능하다. 따라서 '39'는 답으로 가능하다. 34->9도 마찬가지로 4->9 대신 4->39, 14->39대신 14->17로 매칭이 되면 가능하다. 따라서 '9'도 답으로 가능한다.
최종적으로 39와 9를 정렬 한 후 출력해주면 된다.('9 39') 이 때 첫 입력의 간선에서 매칭이 가능한 간선이 하나도 없었다면 역시 -1을 출력해주면 된다. (예외 4 - 코드 134 line)
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
private static final int MAX_NUM = 2000;
private ArrayList<Integer>[] edge;
private ArrayList<Integer> left, right;
private int[] matched;
private boolean[] v;
private HashSet<Integer> findPn() {
boolean[] pnChk = new boolean[MAX_NUM+1];
for (int base = 3; base <= Math.sqrt(MAX_NUM); base+=2) {
if (pnChk[base]) continue;
int tmp = base+base;
while (tmp <= MAX_NUM) {
pnChk[tmp] = true;
tmp+=base;
}
}
HashSet<Integer> pn = new HashSet<>();
for (int i = 3; i <= MAX_NUM; i+=2) {
if (!pnChk[i])
pn.add(i);
}
return pn;
}
private void findEdge() {
edge = new ArrayList[left.size()];
for (int i = 0; i < edge.length; i++)
edge[i] = new ArrayList<>();
// find prime numbers using eratosthenes sieve
HashSet<Integer> pn = findPn();
for (int i = 0; i < left.size(); i++) {
int from = left.get(i);
for (int j = 0; j < right.size(); j++) {
int to = right.get(j);
if (pn.contains(from+to))
edge[i].add(j);
}
}
}
private boolean matching(int from) {
for (int i = 0; i < edge[from].size(); i++) {
int to = edge[from].get(i);
if (v[to]) continue;
v[to] = true;
if (matched[to] == -1 || matching(matched[to])) {
matched[to] = from;
return true;
}
}
return false;
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine());
int first = -1;
// separate even and odd numbers
ArrayList<Integer> even = new ArrayList<>();
ArrayList<Integer> odd = new ArrayList<>();
while (n-->0) {
int cur = Integer.parseInt(st.nextToken());
if ((cur&1)==1) odd.add(cur);
else even.add(cur);
if (first == -1) first = cur;
}
if (even.size() != odd.size()) {
System.out.println(-1);
return;
}
// choice left side and right side
left = (first&1)==1?odd:even;
right = (first&1)==1?even:odd;
// make edge (value compression)
findEdge();
// if someone have 0 edge, there's no answer.
for (int i = 0; i < edge.length; i++) {
if (edge[i].size() == 0) {
System.out.println(-1);
return;
}
}
// bipartite matching
matched = new int[right.size()];
Arrays.fill(matched, -1);
v = new boolean[right.size()];
for (int i = 1; i < left.size(); i++) { // matching except 'first' number.
if (!matching(i)) {
System.out.println(-1);
return;
}
v = new boolean[right.size()];
}
// find answer
ArrayList<Integer> answer = new ArrayList<>(edge[0].size());
for (int i = 0; i < edge[0].size(); i++) {
int to = edge[0].get(i);
if (matched[to] == -1 || matching(matched[to])) {
matched[to] = -1;
answer.add(right.get(to));
}
v = new boolean[right.size()];
}
Collections.sort(answer);
StringBuilder sb = new StringBuilder();
for (int i = 0; i < answer.size(); i++)
sb.append(answer.get(i)).append(' ');
System.out.println(answer.size() == 0 ? -1 : sb);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| 백준 1298 자바 - 노트북의 주인을 찾아서 (BOJ 1298 JAVA) (0) | 2022.01.06 |
|---|---|
| 백준 2188 자바 - 축사 배정 (BOJ 2188 JAVA) (0) | 2022.01.05 |
| 백준 18511 자바 - 큰 수 구성하기 (BOJ 18511 JAVA) (0) | 2022.01.03 |
| 백준 10867 자바 - 중복 빼고 정렬하기 (BOJ 10867 JAVA) (0) | 2022.01.02 |
| 백준 10465 자바 - Rolling Encryption (BOJ 10465 JAVA) (0) | 2022.01.02 |





댓글