문제 : boj13537
기본적으로 알고 있어야 하는 알고리즘 기법들이 좀 있어야 이해할 수 있는 풀이 입니다. 모르는 알고리즘이 있다면 별도로 공부하셔야 이해하실 수 있습니다. 결국 통과된 풀이에 쓰인 오프라인 쿼리는 사실 어차피 값이 변경되지 않으므로, 순서를 바꿔서 쿼리를 진행하더라도 원래 위치만 안다면 순서를 바꿔서 답을 구한 후, 원래 위치에 맞게 답만 출력해주면 된다고만 이해하시면 됩니다. 제곱근 분할법은 여기를 참고하시면 될 것 같습니다. 몰라도 사실 유-명한 세그먼트 트리를 사용하면 더 효율적으로 풀 수 있습니다. (제곱근 분할법인 sqrt(N), 세그먼트 트리는 logN)

1. 시간초과 난 풀이방법
'1'은 오답노트 느낌으로 시간초과 난 풀이방법을 적은 것이니, 통과한 풀이를 보고 싶으시면 '2'로 가시면 됩니다. 일단 머지 소트 트리를 사용하는 문제라고 풀기전에 들어버렸다. 그렇게 들은 이상 쓰고싶지 않았으므로 다른 방법을 찾아봤다.
A값이 1~10^9 이긴 하지만, 결국 N이 최대 100000이므로 A값은 1~100000으로 값을 압축해볼 수 있다. 그리고 update가 별도로 없는 쿼리 문제 이므로 오프라인 쿼리로 처리할 수 있다. 이 때 mo's 알고리즘을 사용하여 오프라인 쿼리를 순서대로 처리하고, 압축된 값을 sqrt decomposition(제곱근 분할법)으로 유지한다면 시간 내에 풀 수 있을 것 같았다. 이 때, 입력받은 k값 이상의 압축된 값을 찾기 위해서 이분 탐색으로 값을 찾도록 했다.
결론적으로 이 풀이법으로는 '시간 초과'가 났고, 제곱근 분할법 대신 세그먼트 트리로도 해봤지만 역시 시간초과가 났다. 아무래도 압축된 값을 찾기 위해 이분 탐색까지 사용하면서 logN 수준의 알고리즘들은 많지만(mo's 적용을 위한 정렬, 세그먼트 트리, 이분 탐색 등) 그게 너무 많았던 것 같다 ㅜ. 아무튼 그렇게 짠 코드는 다음과 같다.
[ 시간 초과를 받은 코드입니다. 통과한 풀이 및 코드는 '2'에서 볼 수 있습니다. ]
import java.io.DataInputStream;
import java.io.IOException;
import java.util.Arrays;
import java.util.HashMap;
import java.util.TreeSet;
public class Main extends FastInput {
class Query implements Comparable<Query> {
int idx, a, b, k, compFactor;
public Query(int idx, int a, int b, int k) {
this.idx = idx;
this.a = a;
this.b = b;
this.k = k;
this.compFactor = a/sqrtN;
}
@Override
public int compareTo(Query o) {
if (this.compFactor == o.compFactor) return this.b - o.b;
return this.compFactor - o.compFactor;
}
}
int n, maxCompVal, prevA, prevB, sqrtN, maxVal;
TreeSet<Integer> existKey = new TreeSet<>();
HashMap<Integer, Integer> comp = new HashMap<>();
Query[] queries;
int[] arr, cnt, bucket, seg;
private void compressionProc(int[] arr) {
int[] tmp = Arrays.copyOf(arr, arr.length);
Arrays.sort(tmp);
maxVal = tmp[tmp.length-1];
int compVal = 1;
for (int i = 1; i <= n; i++) {
if (!comp.containsKey(tmp[i])) {
comp.put(tmp[i], compVal++);
existKey.add(tmp[i]);
}
}
maxCompVal = compVal;
}
private void update(int n, int s, int e, int val, int pm) {
if (val<s || val>e)
return;
seg[n]+=pm;
if (s==e)
return;
int m = (s+e)/2;
update(n*2,s,m,val,pm);
update(n*2+1,m+1,e,val,pm);
}
private void add(int idx) {
int val = comp.get(arr[idx]);
update(1, 1, maxCompVal, val, 1);
}
private void remove(int idx) {
int val = comp.get(arr[idx]);
update(1, 1, maxCompVal, val, -1);
}
private int getAnswer(int n, int s, int e, int l, int r) {
if (s>r || l>e)
return 0;
if (l<=s && e<=r)
return seg[n];
int m = (s+e)/2;
int q1 = getAnswer(n*2, s, m, l, r);
int q2 = getAnswer(n*2+1, m+1, e, l, r);
return q1 + q2;
}
private void initSeg() {
int h = (int) Math.ceil(Math.log(maxCompVal) / Math.log(2));
seg = new int[1<<(h+1)];
}
private int initQuery(Query q) {
prevA = q.a;
prevB = q.b;
for (int i = q.a; i <= q.b; i++) add(i);
if (q.k>maxVal) return 0;
int tmp = comp.get(existKey.ceiling(q.k)) + (comp.containsKey(q.k)?1:0);
if (tmp >= maxCompVal) return 0;
return getAnswer(1, 1, maxCompVal, tmp, maxCompVal);
}
private int query(Query q) {
int curA = q.a;
int curB = q.b;
for (int i = prevA; i < curA; i++) remove(i);
for (int i = curA; i < prevA; i++) add(i);
for (int i = prevB+1; i <= curB; i++) add(i);
for (int i = curB+1; i <= prevB; i++) remove(i);
prevA = curA;
prevB = curB;
if (q.k>maxVal) return 0;
int tmp = comp.get(existKey.ceiling(q.k)) + (comp.containsKey(q.k)?1:0);
if (tmp >= maxCompVal) return 0;
return getAnswer(1, 1, maxCompVal, tmp, maxCompVal);
}
private void solution() throws Exception {
n = nextInt();
sqrtN = (int)Math.sqrt(n);
arr = new int[n+1];
for (int i = 1; i <= n; i++) arr[i] = nextInt();
compressionProc(arr);
initSeg();
int m = nextInt();
queries = new Query[m];
for (int i = 0; i < m; i++) queries[i] = new Query(i, nextInt(), nextInt(), nextInt());
Arrays.sort(queries);
int[] answer = new int[m];
answer[queries[0].idx] = initQuery(queries[0]);
for (int i = 1; i < m; i++) answer[queries[i].idx] = query(queries[i]);
StringBuilder sb = new StringBuilder();
for (int i = 0; i < m; i++) sb.append(answer[i]).append('\n');
System.out.print(sb);
}
public static void main(String[] args) throws Exception {
initFI();
new Main().solution();
}
}
class FastInput {
private static final int DEFAULT_BUFFER_SIZE = 1 << 16;
private static DataInputStream inputStream;
private static byte[] buffer;
private static int curIdx, maxIdx;
protected static void initFI() {
inputStream = new DataInputStream(System.in);
buffer = new byte[DEFAULT_BUFFER_SIZE];
curIdx = maxIdx = 0;
}
protected static int nextInt() throws IOException {
int ret = 0;
byte c = read();
while (c <= ' ') c = read();
do {
ret = ret * 10 + c - '0';
} while ((c = read()) >= '0' && c <= '9');
return ret;
}
private static byte read() throws IOException {
if (curIdx == maxIdx) {
maxIdx = inputStream.read(buffer, curIdx = 0, DEFAULT_BUFFER_SIZE);
if (maxIdx == -1) buffer[0] = -1;
}
return buffer[curIdx++];
}
}
2. 통과한 풀이방법
'1'의 방법으론 더이상 시간을 줄일 방법이 생각나지 않았고, 정리하지 않고 짜서 더이상 답이 안나올 것 같아서 그냥 삭제하고 다시 생각해봤다. '1'은 값을 기준으로 세그먼트 혹은 제곱근 분할법을 적용했지만 생각을 바꿔서 N개의 값을 기준으로 적용했다. 그렇게 하기 위해서 마찬가지로 오프라인 쿼리를 사용했다. 대략적인 로직은 다음과 같다.
A. 입력받은 N개의 수열을 값을 기준으로 내림차순으로 정렬한다.(이 때 정렬 전 위치는 기억해야 함)
B. 입력받은 M개의 쿼리를 마찬가지로 값을 기준으로 내림차순으로 정렬한다.(역시 정렬 전 위치는 기억해야 함)
C. 'B'를 기준으로 각 쿼리의 k값보다 큰 값을 가지는 'A'까지 모두 제곱근 분할법을 통해 위치를 기억해둔다. (이걸 버킷이라 하겠다.)
D. 이제 'C'에서 현재 보고 있는 쿼리에서 i부터 온전한 버킷 부분 이전까지를 답으로 직접 더하고, 온전한 버킷 이후부터 j까지 직접 더한다. 그리고 온전한 버킷들도 더한다.
이후 C와 D를 반복하면서 답을 구하고, 원래 쿼리 순서대로 답을 출력해주면 된다.
이런식이다. A, B, C를 통해 현재 제곱근 분할법을 적용한 A의 위치들은 모두 현재 보고 있는 쿼리의 k 초과값을 가지는 녀석들만 존재하므로 문제없이 답을 구할 수 있다.
예를들어 예제 입력 1은 다음과 같이 진행된다.
5
5 1 2 3 4
3
2 4 1
4 4 4
1 5 2A. 입력받은 N개의 수열을 값을 기준으로 내림차순으로 정렬한다.(이 때 정렬 전 위치는 기억해야 함)

B. 입력받은 M개의 쿼리를 마찬가지로 값을 기준으로 내림차순으로 정렬한다.(역시 정렬 전 위치는 기억해야 함)

C. 'B'를 기준으로 각 쿼리의 k값보다 큰 값을 가지는 'A'까지 모두 제곱근 분할법을 통해 위치를 기억해둔다. (이걸 버킷이라 하겠다.)
-> 'B'에서 정렬한 순서대로 확인하는 것이다. 처음엔 아래와 같이 생겼다. chk는 해당 idx 위치에 현재 보고 있는 쿼리의 k값보다 큰 값을 가지는 A값이 있었는지 체크한다. bucket은 sqrt(N)개로, 해당 위치에 존재하는 chk가 true인 것의 개수를 나타낸다. (세그먼트 트리는 이걸 이진 트리 형태로 더 세분화해서 저장하므로 더 효율적이다. 세그먼트 트리를 안다면 제곱근 분할법에 따른 bucket도 세그먼트 트리의 하위호환 느낌으로 이해하기 쉬울 것이다.)
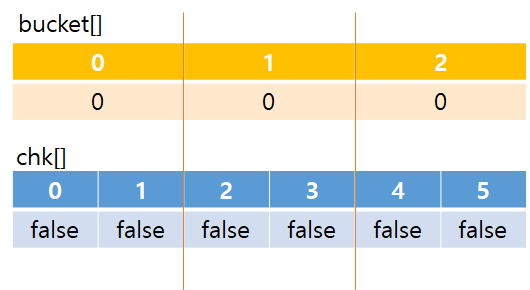
-> '4 4 4' 쿼리를 진행한 후 chk와 bucket은 다음과 같다. k=4 이므로 5이상의 값을 가진 'A'의 값들을 보면 된다. 이 경우 값=5, 원래위치=1 인 녀석 밖에 없으므로 아래와 같이 된다.

D. 이제 'C'에서 현재 보고 있는 쿼리에서 i부터 온전한 버킷 부분 이전까지를 답으로 직접 더하고, 온전한 버킷 이후부터 j까지 직접 더한다. 그리고 온전한 버킷들도 더한다.
-> '4 4 4' 쿼리가 진행된 후의 chk와 bucket을 기준으로 i=4, j=4인 경우 일단 온전한 버킷에 포함되지 않으므로 chk[4]만 확인하면 된다. false이므로 0이 답이다.
C.
-> 이제 쿼리 '1 5 2'를 보면 된다. 우선 'A'에서 구한 것에서 2 초과의 값을 가진 A를 모두 체크한다. (값=4, 원래위치=5), (값=3, 원래위치=4)인 두개를 체크하면 된다. 그럼 다음과 같이 된다.
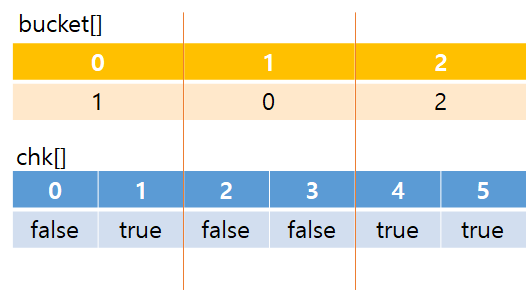
D.
-> 현재 보고 있는 쿼리의 i=1, j=5 이다. 온전한 버킷 이전의 값은 다음과 같다. 1이 된다.

그리고 온전한 버킷 이후의 값은 없고, 온전한 버킷들은 다음과 같다. 직전의 1에 0+2를 더해서 총 3이 된다.
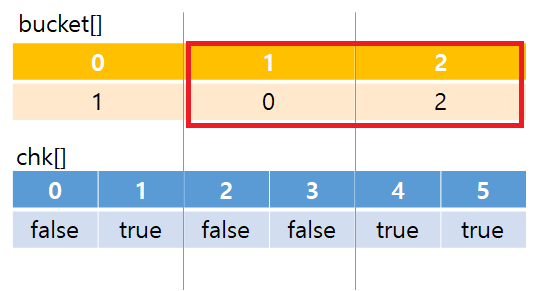
이 때, 만약 i=1, j=4 였다면 다음과 같이 더하면 된다.

C.
-> 다음은 '2 4 1'을 보면 된다. 마찬가지로 값=2, 원래위치=3 인 녀석을 체크한다.

D.
-> i=2, j=4 이므로 다음과 같이 더하면 된다. 답은 2가 된다.

이제 쿼리는 다 봤으니, 최종적으로 'B'에 써둔 원래 위치를 기준으로 답을 순서대로 출력해주면 다음과 같이 정답이 된다.
2
0
3
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
class A implements Comparable<A> {
int idx, k;
public A(int idx, int k) {
this.idx = idx;
this.k = k;
}
@Override
public int compareTo(A o) {
return o.k - this.k;
}
}
class Query implements Comparable<Query> {
int idx, a, b, k;
public Query(int idx, int a, int b, int k) {
this.idx = idx;
this.a = a;
this.b = b;
this.k = k;
}
@Override
public int compareTo(Query o) {
return o.k - this.k;
}
}
public class Main {
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
A[] arr = new A[n+1];
arr[0] = new A(-1, 0);
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) arr[i] = new A(i, Integer.parseInt(st.nextToken()));
Arrays.sort(arr);
int m = Integer.parseInt(br.readLine());
Query[] queries = new Query[m];
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
queries[i] = new Query(i,
Integer.parseInt(st.nextToken()),
Integer.parseInt(st.nextToken()),
Integer.parseInt(st.nextToken()));
}
Arrays.sort(queries);
boolean[] chk = new boolean[n+1];
int sqrtN = (int)Math.sqrt(n);
int[] bucket = new int[1000];
int[] answer = new int[m];
for (int i = 0, j = 0; i < m; i++) {
Query q = queries[i];
// update
while(j <= n && arr[j].k > q.k) {
chk[arr[j].idx] = true;
bucket[arr[j].idx/sqrtN]++;
j++;
}
// get answer
int sum = 0;
int a = q.a;
int b = q.b;
while (a%sqrtN!=0 && a<=b) if (chk[a++]) sum++;
while ((b+1)%sqrtN!=0 && a<=b) if (chk[b--]) sum++;
for (int z = a/sqrtN; z < (b+1)/sqrtN; z++) sum += bucket[z];
answer[q.idx] = sum;
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < m; i++) sb.append(answer[i]).append('\n');
System.out.print(sb);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| 백준 16955 자바 - 오목, 이길 수 있을까? (boj 16955 java) (0) | 2022.03.26 |
|---|---|
| 백준 20420 자바 - 화살표 미로 (Normal) (BOJ 20420 JAVA) (0) | 2022.03.25 |
| 백준 1417 자바 - 국회의원 선거 (BOJ 1417 JAVA) (0) | 2022.03.24 |
| 백준 17756 자바 - Kieszonkowe (BOJ 17756 JAVA) (0) | 2022.03.24 |
| 백준 2003 자바 - 수들의 합 2 (BOJ 2003 JAVA) (0) | 2022.03.23 |





댓글