문제 : boj2143
1.
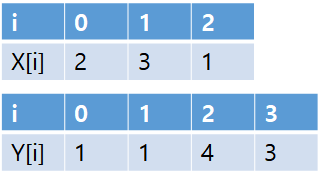
부 배열을 이따 생각하고, 일단 X랑 Y라는 두 배열이 있는데 두 배열의 각 원소를 하나씩 더한 합이 T가 되는 경우부터 생각해보자. 아래와 같은 X, Y 배열이 있다.
1.1
가장 간단히 X[i] + Y[j] 가 T가 되는걸 찾는 방법은 모든 X의 원소에 대해 Y의 모든 경우의 수를 전부 확인해보면 된다. X[0]+Y[0] 확인, X[0]+Y[1] 확인, ... , X[1]+Y[0] 확인, X[1]+Y[1]확인, ... X[2]+Y[3] 확인.
이 경우 X의 개수 * Y의 개수 만큼 봐야 한다. O(XY)
1.2
1.1보다 더 빠르게 할 수 있는 방법이 있다. Y를 정렬한 후 O(YlogY), 각 X에 대해 T-X[i]가 Y에 있는지를 이분탐색으로 찾는 방식이다. 이 경우 O(YlogY + XlogY) = O((X+Y)logY) 정도가 걸린다.
1.3
1.2보다 더 빠르게 할 수 있다. Y를 해싱한 후 O(Y), 각 X에 대해 T-X[i]가 해시된 값에 있는지를 바로 찾는 것이다. 이 경우 O(X+Y) 정도가 걸린다.
2.
자 그럼 이제 A의 부배열을 전부 계산해서 X로, B의 부배열을 전부 계산해서 Y로 만든다면 '1'의 로직 중 하나를 써서 답을 구할 수 있다. 다만 A와 B의 부배열은 각각 총 1000*1000개가 나오므로, '1.1'로는 시간내에 통과할 수 없다. 따라서 '1,2'나 '1.3'을 써야 하고, 언어에 따라 메모리가 부족하다면 '1.2'를 쓰면 된다. 자바로는 '1.3'으로 충분히 통과 가능해서 '1.2'는 가능성만 생각해보고 해보진 않았다. 이론상(?) 당연히 '1.2'도 시간내에 될꺼다.
그럼 부배열 전체의 값을 계산해보자. 일단 A를 입력받으면서 prefixSum 배열로 만든다. '1 3 1 2'가 들어왔다면 다음과 같이 될꺼다.

그렇다면 이제 A의 임의의 두 인덱스에 대해 그 사이의 합을 쉽게 구할 수 있다. 그럼 2중 반복문으로 모든 범위를 확인해보면 O(A^2)으로 모든 경우를 살펴보면서 A의 모든 부배열의 합을 구할 수 있다. 그럼 구한 합을 HashMap에 넣는다. 이 때 key는 부배열의 합, value는 해당 합이 나타난 횟수이다. 따로 value로 나온 횟수도 기록해두는 이유는, 어떠한 두 부배열의 합이 같더라도 서로 다른 부배열 이므로 따로 카운팅해야 하기 때문이다.
B도 마찬가지로 prefixSum을 진행하며 입력받는다. 그리고 마찬가지 방식으로 부배열의 합을 O(B^2)으로 구하면서, 'T-해당합'이 HashMap에 존재한다면 결과에 더해넣어주면 된다.
3.
T도 +-10억까지이고, A나 B도 모든 수를 합쳐봐야 절대값이 10억을 넘지 못한다. 따라서 연산의 결과나 중간과정에서 int 범위를 넘어설 일은 없다. 다만 결과를 카운팅 할 때, 카운팅한 결과값은 int 범위를 넘어갈 수 있으므로 (대충 1000C2 * 1000C2) 저처럼 안틀리려면 카운팅은 long으로 하세요 ㅠ
코드 : github
import java.io.DataInputStream;
import java.io.IOException;
import java.util.HashMap;
public class Main extends FastInput {
private void solution() throws Exception {
int t = nextInt();
int n = nextInt();
int[] arr = new int[n+1];
for (int i = 1; i <= n; i++) {
arr[i] = arr[i-1] + nextInt();
}
HashMap<Integer, Integer> hm = new HashMap<>();
for (int i = 1; i <= n; i++) {
for (int j = i; j <= n; j++) {
int rangeSum = arr[j]-arr[i-1];
hm.put(rangeSum, !hm.containsKey(rangeSum) ? 1 : hm.get(rangeSum)+1);
}
}
int m = nextInt();
arr = new int[m+1];
for (int i = 1; i <= m; i++) {
arr[i] = arr[i-1] + nextInt();
}
long answer = 0l;
for (int i = 1; i <= m; i++) {
for (int j = i; j <= m; j++) {
int rangeSum = arr[j]-arr[i-1];
int key = t-rangeSum;
if (hm.containsKey(key)) {
answer += hm.get(key);
}
}
}
System.out.println(answer);
}
public static void main(String[] args) throws Exception {
initFI();
new Main().solution();
}
}
class FastInput {
private static final int DEFAULT_BUFFER_SIZE = 1 << 16;
private static DataInputStream inputStream;
private static byte[] buffer;
private static int curIdx, maxIdx;
protected static void initFI() {
inputStream = new DataInputStream(System.in);
buffer = new byte[DEFAULT_BUFFER_SIZE];
curIdx = maxIdx = 0;
}
protected static int nextInt() throws IOException {
int ret = 0;
byte c = read();
while (c <= ' ') c = read();
boolean neg = (c == '-');
if (neg) c = read();
do {
ret = ret * 10 + c - '0';
} while ((c = read()) >= '0' && c <= '9');
if (neg) return -ret;
return ret;
}
private static byte read() throws IOException {
if (curIdx == maxIdx) {
maxIdx = inputStream.read(buffer, curIdx = 0, DEFAULT_BUFFER_SIZE);
if (maxIdx == -1) buffer[0] = -1;
}
return buffer[curIdx++];
}
}
'PS > BOJ' 카테고리의 다른 글
| 백준 9327 자바 - 용량 확보 (BOJ 9327 JAVA) (0) | 2021.12.13 |
|---|---|
| 백준 9213 자바 - 꽤 좋은 수 (BOJ 9213 JAVA) (0) | 2021.12.13 |
| 백준 2014 자바 - 소수의 곱 (BOJ 2014 JAVA) (0) | 2021.12.12 |
| 백준 14413 자바 - Poklon (BOJ 14413 JAVA) (0) | 2021.12.11 |
| 백준 7585 자바 - Brackets (BOJ 7585 JAVA) (0) | 2021.12.11 |





댓글