문제 : boj2749
일단 10^18 이므로 그냥 구하기는 절대로 불가능한 수치임을 알 수 있다 ㅋㅋㅋ. 내 경우엔 피보나치의 경우 행렬의 거듭 제곱으로 풀 수 있다는걸 이미 알고 있었으므로 공식만 찾아서 풀었다. 공식은 f(n)이 n번째 피보나치라 할 때, 아래와 같다.
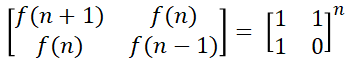
이 때 거듭 제곱의 계산은, 분할 정복을 활용해서 O(logN)에 빠르게 구할 수 있다. 예를들어 A^8 = ((A^2)^2)^2 임을 활용하는 것이다. 혹시 모른다면 예전에 백준 게시판에 답글달았던 이 글을 참고하면 된다.
그보다, 다른분의 풀이도 보다보니 '피사노 주기'라는 것도 알게 되었다. 피보나치 수를 어떠한 수로 나눈 나머지는 항상 주기성을 가진다고 한다. 수의 세계는 신비로운 것 같다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private static final long MOD = 1000000l;
private long[][] matrixMult(long[][] a, long[][] b) {
long[][] arr = new long[2][2];
arr[0][0] = (a[0][0]*b[0][0]%MOD + a[0][1]*b[1][0]%MOD)%MOD;
arr[1][0] = (a[0][0]*b[0][1]%MOD + a[0][1]*b[1][1]%MOD)%MOD;
arr[0][1] = (a[1][0]*b[0][0]%MOD + a[1][1]*b[1][0]%MOD)%MOD;
arr[1][1] = (a[1][0]*b[0][1]%MOD + a[1][1]*b[1][1]%MOD)%MOD;
return arr;
}
private long[][] fibo(long n) {
if (n == 1) {
long[][] arr = {{1,1},{1,0}};
return arr;
}
long[][] tmp = fibo(n/2);
if (n%2==1) {
return matrixMult(matrixMult(tmp, tmp), fibo(1));
} else {
return matrixMult(tmp, tmp);
}
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
long n = Long.parseLong(br.readLine());
System.out.println(fibo(n)[0][1]);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| 백준 9613 자바 - GCD 합 (boj 9613 java) (0) | 2022.04.06 |
|---|---|
| 백준 1486 자바 - 등산 (boj 1486 java) (0) | 2022.04.05 |
| 백준 1072 자바 - 게임 (boj 1072 java) (0) | 2022.04.05 |
| 백준 1644 자바 - 소수의 연속합 (boj 1644 java) (0) | 2022.04.05 |
| 백준 15927 자바 - 회문은 회문아니야!! (boj 15927 java) (0) | 2022.04.04 |





댓글