문제 : https://www.acmicpc.net/problem/3409
코드 : https://github.com/NaHwaSa/BOJ_BaekjunOnlineJudge/blob/master/03400/BOJ_3409.java
첫 다이아 티어 성공한 문제이다. 사실 골드나 플래도 제대로 못풀다보니 다이아급은 쳐다도 안봤었는데 얼마나 어려운지 볼려고 도전해봤다(보통 티어랑 알고리즘 분류는 끄고푸는데, 문제 검색을 실버, 골드, 플래 전체 체크하고 순서 랜덤으로 두고 검색해서 푸는 편임). 결과는 의외로 쉬웠다. 안쫄고 이제 다야도 한번 덤벼봐야겠다. 풀고보니 다른 분들은 DP(다이나믹 프로그래밍)으로 다들 분류를 설정해뒀던데 내 경우엔 그냥 dfs로 풀었다.
이 문제의 경우 문제만 놓고 보면 복잡해보일 수 있는데, 그려놓고 보면 의외로 쉽다. root node는 '다음 줄에는 어떤 변수가 T인지 주어진다.' 부분에서 입력받은 노드이다. '예제 입력 1'을 그래프(트리) 형태로 그려보면 다음과 같다.

이렇게 트리를 그린다고 생각하고, 전위순회 하듯이 탐색을 하면 된다. 이 때, leaf node는 'A = 알파벳 소문자로 이루어져 있는 단어'의 형태로 입력 받은 경우이다. leaf node가 아니라면 다음 탐색으로만 진행하고, leaf node를 만난다면 p와 비교를 진행하면 된다.(그럼 실제로 방정식을 풀어 t를 만들어두고 p와 비교하는 것과 동일한 동작을 하면서, 당연하게도 시간복잡도 및 메모리복잡도 면으로도 효율적이다.)
탐색은 전위순회이므로 dfs로 하면 된다. 그럼 위 그림에서 탐색을 진행해보겠다.
예제 입력 1에서 p=debate 였다.
일단 START = FIRST + SECND 이므로 FIRST로 진행한다. FIRST는 leaf node가 아니고, FIRST = D + E 이므로 D로 진행한다. leaf node에서 "good"을 만났다.

'pIdx'는 p의 한 문자를 가르키는 포인터이다.

현재 leaf node에서 만난 "good"의 character를 순서대로 진행하며, 현재 pIdx가 가르키고 있는 p의 character와 동일하다면 찾은것이다. 그럼 pIdx를 1 증가시켜주는 식으로 비교하면 된다.

다음 순회를 진행한다. 이번엔 E를 본다.
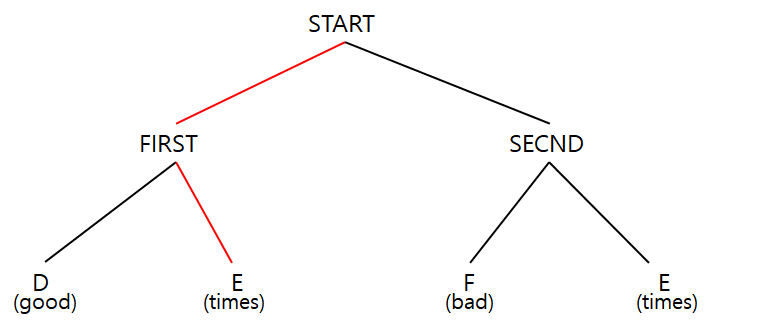
마찬가지로 p와 비교를 진행한다. 이 때 pIdx는 초기화 되지 않는다. 다음 테스트케이스로 넘어가야만 초기화 된다. 그러니, p의 'e' 부터 비교가 되는 것이다.

다음은 START에서 우측으로 진행해서 SECND로 가고, 거기서 다시 좌측으로 진행하여 F를 본다. 비교도 마찬가지 방식으로 진행한다.

마지막으로 SECND의 우측인 E를 확인한다.

이렇게 모든 위치를 순회하고, 비교 결과 p의 모든 글자를 찾았다면 "YES"가 되고, 아니면 "NO"가 되는 것이다.
그럼 이렇게 짜면 되는데, 이렇게만 하면 사실 시간초과가 난다. 일반적으로 bfs, dfs 하듯이 방문 체크를 해줘야겠는데, 이 부분이 좀 생각하는데 시간이 걸렸다. 결론적으로 각 노드에 대해 방문체크를 하긴 하는데, 뭐라도 하나 찾아지면 방문체크를 다시 처음부터 해야한다. 왜냐면 pIdx가 바뀌면, 이전에 방문했을 때 매칭되는 문자를 못찾았단 녀석들도 찾을 수 있게 될 수 있기 때문이다.
예를들어 위에서 설명했던 그림에서 맨 아랫줄 리프노드만 봤을때 'D D D D D ... E D D D D ... F' 이런식으로 있다. 이 때 사실 p는 E, F랑 전부 매칭이 되는 경우, D를 매번 체크해주는것은 당연히 손해이다. 이럴 때 방문체크를 통해 D 부분을 전부 방문하지 않을 수 있다. 그러나 E를 만나서 pIdx가 변경되었다면, 이제 D에서도 어쩌면 매칭되는 문자가 생길 수 있다. 따라서 방문체크를 해제해줘야 한다. 그리고 E다음의 D와 만나서 체크가 끝나면 다시 방문체크가 되면서 F까지 편안하게(?) 진행할 수 있다.
그럼 이제 이걸 코드로 구현하면 된다. 전체적으로 딱히 설명이 필요할만한 알고리즘적 지식이 사용되지 않았으므로, 구현부분에 대해서는 코드만 보면 문제없이 이해할 수 있을 것이다.
'PS > BOJ' 카테고리의 다른 글
| 백준 2696 자바 - 중앙값 구하기 (BOJ 2696 JAVA) (0) | 2021.10.29 |
|---|---|
| 자바 6137 자바 - 문자열 생성 (BOJ 6137 JAVA) (0) | 2021.10.29 |
| 백준 1575 자바 - 졸업 (BOJ 1575 JAVA) (0) | 2021.10.26 |
| 백준 16499 자바 - 동일한 단어 그룹화하기 (BOJ 16499 JAVA) (0) | 2021.10.26 |
| 백준 14881 자바 - 물통 문제 (BOJ 14881 JAVA) (0) | 2021.10.25 |





댓글