문제 : boj1048

필요 알고리즘 개념
- 다이나믹 프로그래밍 (DP, 동적계획법)
- 대부분의 경우의 수 문제는 DP로 풀 수 있다. 이 문제도 DP로 풀 수 있다.
- 누적합
- 유니콘의 이동 범위 내의 누적합을 구하기 위해 2차원 누적합을 사용하면 빠르다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
이 문제 설명이 약간 부족한데, 시작은 어느지점에서 해도 된다! 이것때매 좀 헷갈렸다.
우선 DP를 어떤식으로 진행하는지는 알아야 풀 수 있다. 그리고 2차원 누적합을 알아야하는데, '누적 합(prefix sum), 2차원 누적합(prefix sum of matrix)' 글을 보면 알 수 있다. 그리고 나머지 연산의 규칙도 알아야하는데, 아래와 같다. 아무튼 덧셈이나 뺄셈이나 곱셈이나 중간 연산중에 M으로 나눠줘서 계산해도 결과에 영향을 끼치지 않는다는점만 알면 된다.

1. 유니콘은 일단 잊고, 1차원에서 단순하게 이동할 때를 먼저 생각해보자.
원래 복잡해 보이는 문제는 단순화시켜서 생각해보면 의외로 논리가 복잡하지 않은 경우가 많다.
BABAB라는 문자열이 있고, 좌우로만 이동 가능할 때 ABA 순서대로 찾는다고 해보자.
dp[a][b]를 a는 찾고자하는 "ABA"의 각 문자 번호를 뜻하고, b는 "ABABA"의 각 문자 번호를 뜻한다고 하자. dp[a][b]는 a번 문자까지 봤을 때, b번 글자 부분까지 도달했을 때의 경우의 수 이다.
그럼 우선 dp[1][b] 부분은 다음과 같이 될 것이다. "ABA"중 'A'만 봤을 때 각 b번 문자열까지 도달했을 때 경우의 수이므로, 당연히 "BABAB" 중 'A'가 있던 위치만 1개의 경우가 있을 것이다.

다음으로 ABA 중 'B'를 생각해보자. 좌우로만 이동가능하다고 했으므로, 이전값(a=1일때의 값)에서 b-1과 b+1의 값들을 가져와 모두 합치면 될 것이다.

마지막 'A'도 동일하다! 최종적으로 답은 6이 될 것이다.

2. 2차원으로 확장해도 동일하다.
2차원에서 상하좌우로 움직일 수 있다면 달라지는게 있을까? dp[a][b]만 dp[a][b][c]로 바꾸면 될 것이다. b와 c는 몇 번째 입력된 문자열의 c번째 문자를 뜻하게 된다. 논리는 동일하다. 이전 a값 dp 배열에서 상하좌우에서 경우의수를 가져와 합쳐주면 된다. 빨간색 부분은 이전 계산 결과에서 노란색 부분들의 경우의 수의 합이면 된다.


3. 그럼 이제 상하좌우 대신 유니콘의 이동 방식을 대입하면 된다.
유니콘의 이동 방식을 그림으로 보면 다음과 같다. 복잡하지만, 위 상하좌우에서 가져오던과 동일하다. 빨간 부분에 올 수 있는 지점은 노란색 지점이므로, 노란색 지점의 경우의수의 합이 빨간색에 들어가면 된다.
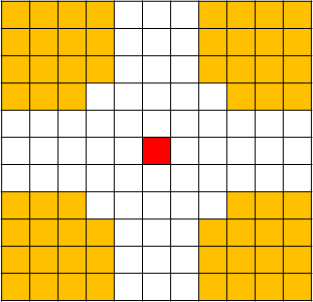
4. 물론 노란색 부분의 합을 완전 탐색으로 모두 더해주면 시간초과난다.
노란색 부분의 경우의수를 합쳐주는것만 O(NM)이 필요하고, 모든 칸에 대해 찾으려는 단어 길이만큼 봐야 하므로 시간복잡도는 O(50 x (NM)^2) 이 필요하다. 대략 O(4천억) 이므로 모든 경우를 보는건 불가하다. 그럼 저 노란 부분의 합을 빠르게 구할 수 있어야 한다. 2차원 누적합을 응용해서 적용하면 빠르게 구할 수 있다. 그럼 O(50 x NM) 정도로 가능하다.
전체의 누적합에서 파란부분의 2차원 누적합을 빼주고(보라색 부분도 포함임), 빨간색 부분도 빼주고(보라색 포함), 보라색은 파란색과 빨간색에서 2번 빼졌으므로 1번 더해준다. 그리고 녹색 부분을 빼주면 된다.

private long cases(long[][] bf, int i, int j) {
long answer = bf[r][c]; // 전체 누적합
answer -= get2dRangeSum(bf, i-1, 1, i+1, c); // 빨간부분
answer -= get2dRangeSum(bf, 1, j-1, r, j+1); // 파란부분
answer += get2dRangeSum(bf, i-1, j-1, i+1, j+1); // 보라부분
answer -= get2dRangeSum(bf, i-2, j-2, i-2, j-2); // 이하 녹색부분
answer -= get2dRangeSum(bf, i+2, j-2, i+2, j-2);
answer -= get2dRangeSum(bf, i-2, j+2, i-2, j+2);
answer -= get2dRangeSum(bf, i+2, j+2, i+2, j+2);
return positiveModResult(answer);
}
따라서 매번 이전 값의 2차원 누적합을 가지고 위에서 설명한대로 유니콘의 이동 반경 부분의 경우의수를 합쳐준다. 그리고 다음 문자를 보기 전에 누적합을 계산해주고 넘어간다.
for (int k = 1; k < len; k++) {
// for each alphabet of base
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= c; j++) {
if (map[i][j] != base.charAt(k)) continue;
dp[k][i][j] = cases(dp[k-1], i, j); // 이전값(dp[k-1])을 가지고 현재값을 구함
}
}
// 위에서 모든값을 계산한 후, 다음 문자를 보기 전에 누적합 계산
// prefix sum
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= c; j++) {
dp[k][i][j] += dp[k][i-1][j] + dp[k][i][j-1] - dp[k][i-1][j-1];
dp[k][i][j] = positiveModResult(dp[k][i][j]);
}
}
}
5. 주의점
초반부에 말한듯이, 중간중간 연산의 결과를 1,000,000,007(이하 MOD)로 나눈 나머지만 남겨도 결과를 구하는데 영향을 끼치지 않는다. long 범위도 아득히 넘어가므로 매번 MOD로 나눈 나머지만 유지해야 한다.
이 때, 파이썬을 제외한 대부분의 언어들은 음수값에 대해 나머지 연산이 수학적으로 제대로 지원되지 않는다. 자바도 마찬가지다. 따라서 MOD로 나눈 나머지를 구하기 전에 항상 양수로 만들어줘야한다. 이거때문에 1시간동안 맞왜틀을 외쳤다 ㅠㅠ.

이건 어떻게 바꾸냐면, A%M = (A+M)%M 인걸 이용한다(M%M=0 이므로 더해도 동일하다).
private long positiveModResult(long in) {
while (in < 0) in += MOD;
return in%MOD;
}
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private static final BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 1<<16);
private static final int MOD = 1_000_000_007;
private int r, c;
public static void main(String[] args) throws Exception {
new Main().solution();
}
public void solution() throws Exception {
StringTokenizer st = new StringTokenizer(br.readLine());
r = Integer.parseInt(st.nextToken());
c = Integer.parseInt(st.nextToken());
int l = Integer.parseInt(st.nextToken());
String base = br.readLine();
int len = base.length();
if (checkInvalidity(l, base, len)) {
System.out.println(0);
return;
}
long[][][] dp = new long[len][r+1][c+1];
char[][] map = new char[r+1][c+1];
init(r, c, base, dp, map);
for (int k = 1; k < len; k++) {
// for each alphabet of base
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= c; j++) {
if (map[i][j] != base.charAt(k)) continue;
dp[k][i][j] = cases(dp[k-1], i, j);
}
}
// prefix sum
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= c; j++) {
dp[k][i][j] += dp[k][i-1][j] + dp[k][i][j-1] - dp[k][i-1][j-1];
dp[k][i][j] = positiveModResult(dp[k][i][j]);
}
}
}
System.out.println(dp[len-1][r][c]);
}
private boolean checkInvalidity(int l, String base, int len) {
for (int i = 0; i < len; i++) {
if (base.charAt(i)-'A'+1 > l) {
return true;
}
}
return false;
}
private void init(int r, int c, String base, long[][][] dp, char[][] map) throws Exception {
for (int i = 0; i < r; i++) {
String row = br.readLine();
for (int j = 0; j < c; j++) {
map[i+1][j+1] = row.charAt(j);
dp[0][i+1][j+1] = (map[i+1][j+1]== base.charAt(0) ? 1:0) + dp[0][i][j+1] + dp[0][i+1][j] - dp[0][i][j];
}
}
}
private long cases(long[][] bf, int i, int j) {
long answer = bf[r][c];
answer -= get2dRangeSum(bf, i-1, 1, i+1, c);
answer -= get2dRangeSum(bf, 1, j-1, r, j+1);
answer += get2dRangeSum(bf, i-1, j-1, i+1, j+1);
answer -= get2dRangeSum(bf, i-2, j-2, i-2, j-2);
answer -= get2dRangeSum(bf, i+2, j-2, i+2, j-2);
answer -= get2dRangeSum(bf, i-2, j+2, i-2, j+2);
answer -= get2dRangeSum(bf, i+2, j+2, i+2, j+2);
return positiveModResult(answer);
}
private long get2dRangeSum(long[][] arr, int r1, int c1, int r2, int c2) {
if (r1==r2 && c1==c2 && (r1<=0||r1>r||c1<=0||c1>c)) return 0;
if (r1==0) r1=1; if (r1==r+1) r1=r;
if (r2==0) r2=1; if (r2==r+1) r2=r;
if (c1==0) c1=1; if (c1==c+1) c1=c;
if (c2==0) c2=1; if (c2==c+1) c2=c;
long answer = arr[r2][c2]-arr[r1-1][c2]-arr[r2][c1-1]+arr[r1-1][c1-1];
return positiveModResult(answer);
}
private long positiveModResult(long in) {
while (in < 0) in += MOD;
return in%MOD;
}
}'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 1194 - 달이 차오른다, 가자. (java) (0) | 2023.03.06 |
|---|---|
| [자바] 백준 18513 - 샘터 (java) (2) | 2023.03.03 |
| [자바] 백준 23807 - 두 단계 최단 경로 3 (java) (0) | 2023.03.01 |
| [자바] 백준 2072 - 오목 (java) (0) | 2023.02.27 |
| [자바] 백준 27453 - 귀엽기만 한 게 아닌 한별 양 (java) (0) | 2023.02.24 |





댓글