목차
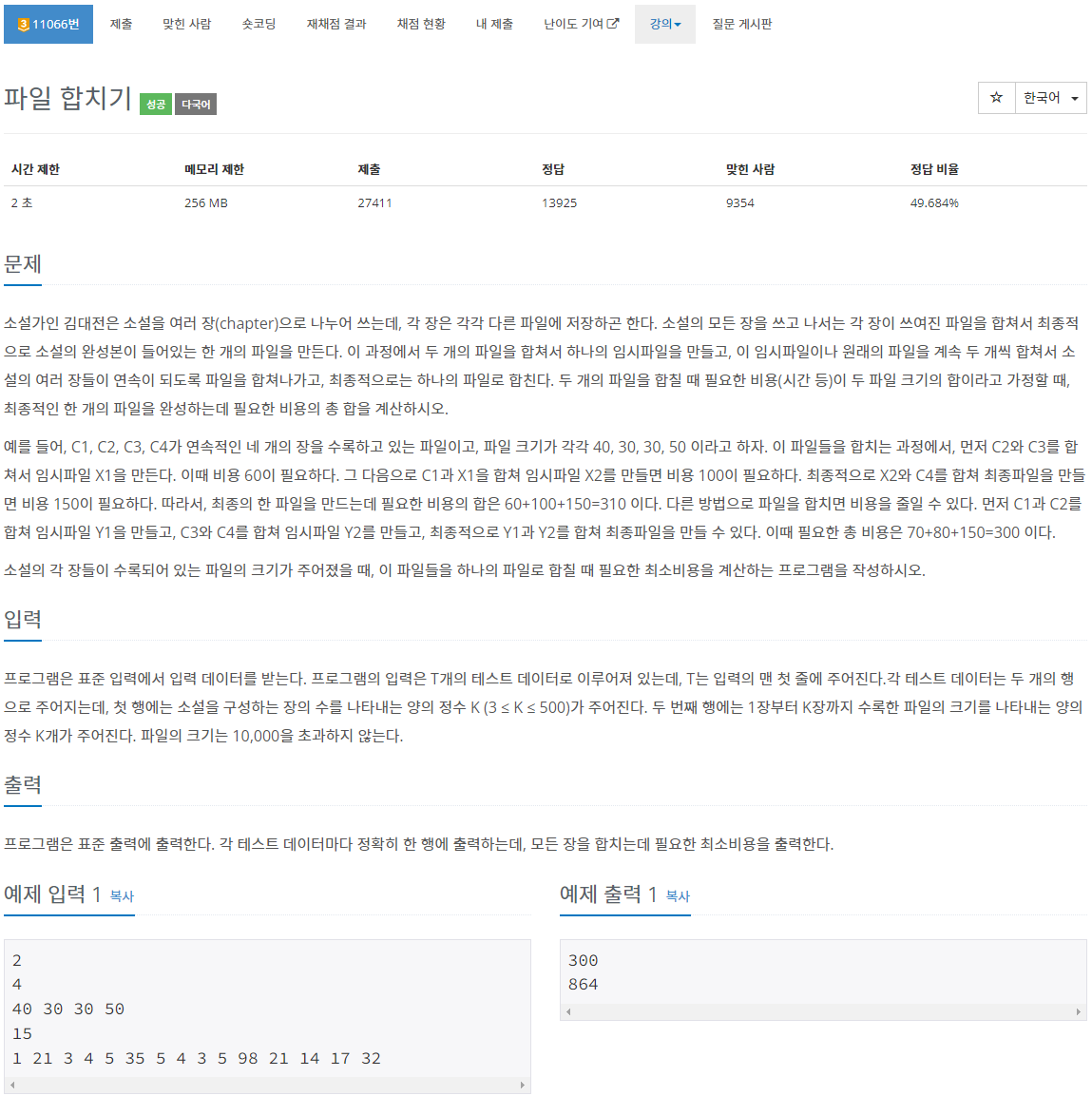
문제 : boj11066
필요 알고리즘
- 다이나믹 프로그래밍 (DP, 동적 계획법), 누적합
- 분할정복 느낌으로 생각해보면 풀이법을 찾을 수 있다. 그리고 구현을 위해 DP와 누적합을 사용해야 한다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
우선, 이 문제의 경우 연속된 파일끼리만 합칠 수 있다는 점을 주의해야 한다. 만약 아무 파일이나 합칠 수 있었다면 그리디로 매번 합쳐진 파일들 중 가장 가중치가 낮은 2개를 합치는 방식으로 풀어야 하는 문제이다. 그리고 누적합을 어떻게 구하는지 모른다면 '이 글'을 참고해보자.
풀이는 들어보면 간단한데, 바로 생각하기는 개인적으로 쉽지 않았던 것 같다. 내 경우엔 분할 정복으로 생각해서 풀었다. 하나씩 합쳐가다면서 전체를 만드는 방식으로 생각했다. 만약 2개의 파일 F1, F2를 합치는 경우 최소 비용은 그냥 F1+F2가 될 것이다. 그럼 파일이 3개라면 어떨까? (F1+F2)+F3 또는 F1+(F2+F3) 의 비용 중 낮은 비용을 골라야 할꺼다.
그럼 4개면 어떨까?
1. F1+(F2+(F3+F4))
2. (F1+F2)+(F3+F4)
3. ((F1+F2)+F3)+F4
위의 경우 중 최소 비용을 고르면 답이 될 것이다.
즉, 파일이 N개일 경우 최소 비용은
1. F1+(F2~Fn의 합)
2. (F1~F2의 합) + (F3~Fn의 합)
3. (F1~F3의 합) + (F4~Fn의 합)
...
N. (F1~Fn-1의 합)+Fn
중 최소비용을 고르면 된다. 그리고 예를들어 저 중 (F2~Fn의 최소비용)을 알기 위해서는 F2~Fn에 포함된 N-1개의 파일의 최소비용을 알아야 한다. 즉 재귀적으로 점점 더 작은 조합의 최소 비용을 알아야 하고, 그렇다면 메모리에 특정 구간의 최소비용을 저장해 두는 것이 효과적일 것이다.
따라서 dp[A][B]를 A~B의 최소비용이라고 하자. 그리고 파일이 1개일 때부터 시작해 점점 증가하면서 2개, 3개, 4개, ... N개를 계산해 나간다면 재귀적인 처리 없이 항상 원하는 데이터를 가지고 있을테니 효율적이다. 위의 내용을 이해했다면 사실 그대로 구현하면 된다. 이하 내가 구현한 방식은 주석으로 작성하였다.
private int solve() throws Exception {
int n = Integer.parseInt(br.readLine());
int[] arr = new int[n];
int[] prefixSum = new int[n];
int[][] dp = new int[n][n]; // 위에서 말한 dp[A][B]이다. A~B의 최소비용을 뜻한다.
for (int[] row : dp) Arrays.fill(row, INF);
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
dp[i][i] = 0; // 파일 1개일 때의 최소비용은 0으로 초기화해둔다.
}
prefixSum[0] = arr[0]; // 누적합을 미리 구해둔다. F1+(F2+F3)일 경우 최종 비용은 F1+(F2+F3)*2 가 된다. 이 중복되는 부분을 처리하기 위해서다.
for (int i = 1; i < n; i++) prefixSum[i] = arr[i] + prefixSum[i - 1];
for (int gap = 1; gap < n; gap++) { // gap은 s부터 시작해 몇 개의 파일을 합칠지를 나타낸다.
for (int s = 0; s < n - gap; s++) { // 현재 몇 번 파일을 보고 있는지를 뜻한다.
for (int i = s; i < s+gap; i++) { // 어떤 파일을 합칠지 정하기 위한 중간지점을 나타낸다.
dp[s][s+gap] = Math.min(dp[s][s+gap], dp[s][i] + dp[i+1][s+gap] + prefixSum[s+gap] - (s==0?0:prefixSum[s-1]));
// s부터 s+gap까지의 최소비용은 [s에서 i까지의 최소비용] + [i+1부터 s+gap까지의 최소비용] + [중복된 부분 처리용 누적합 더하기] 들 중 최소값이다.
}
}
}
return dp[0][n - 1];
}
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 1<<16);
static final int INF = Integer.MAX_VALUE/3-1;
public static void main(String[] args) throws Exception {
new Main().solution();
}
private void solution() throws Exception {
int t = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
while (t-->0) sb.append(solve()).append('\n');
System.out.print(sb);
}
private int solve() throws Exception {
int n = Integer.parseInt(br.readLine());
int[] arr = new int[n];
int[] prefixSum = new int[n];
int[][] dp = new int[n][n];
for (int[] row : dp) Arrays.fill(row, INF);
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
arr[i] = Integer.parseInt(st.nextToken());
dp[i][i] = 0;
}
prefixSum[0] = arr[0];
for (int i = 1; i < n; i++) prefixSum[i] = arr[i] + prefixSum[i - 1];
for (int gap = 1; gap < n; gap++) {
for (int s = 0; s < n - gap; s++) {
for (int i = s; i < s+gap; i++) {
dp[s][s+gap] = Math.min(dp[s][s+gap], dp[s][i] + dp[i+1][s+gap] + prefixSum[s+gap] - (s==0?0:prefixSum[s-1]));
}
}
}
return dp[0][n - 1];
}
}
'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 11912 - 격자 보존하기 (java) (0) | 2023.08.11 |
|---|---|
| [자바] 백준 2138 - 전구와 스위치 (java) (0) | 2023.08.11 |
| [자바] 백준 14550 - 마리오 파티 (java) (0) | 2023.08.09 |
| [자바] 백준 14938 - 서강그라운드 (java) (0) | 2023.08.08 |
| [자바] 백준 1311 - 할 일 정하기 1 (java) (0) | 2023.08.03 |





댓글