문제 : boj11660
prefix sum을 이용하는 문제이다. 1차원 배열에 대해 prefix sum을 계산해두면 1차원 배열의 모든 구간에 대한 구간합을 O(1)로 구할 수 있다. 따라서 모든 행에 포함된 열에 대해 행의 개수만큼 prefix sum을 계산해둔다면, O(MN)으로 문제를 풀 수 있다. 이렇게 짠 코드는 여기(github)에 있다. 이하 풀이는 2차원 prefix sum을 사용한 풀이이다.
2차원 배열에 대해 prefix sum을 유지한다면 O(M)으로도 가능하다. arr[a][b]를 (1, 1)부터 (a, b) 까지의 합이라고 정의하자.

그럼 arr[a][b] = '[a. b]의 값' + arr[a-1][j] + arr[a][b-1] - arr[a-1][b-1] 이라고 할 수 있다. '-arr[a-1][b-1]' 부분은 두 번 더해졌으므로 한 번 빼준 것이다.
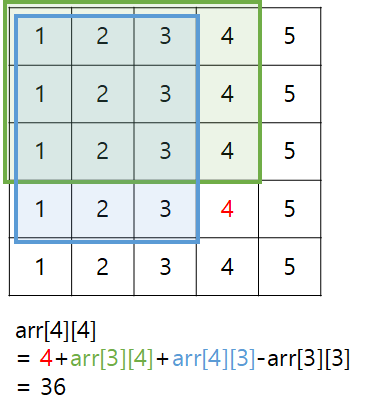
위의 공식을 적용한다면, 입력을 받으면서 바로바로 arr[a][b]를 계산해줄 수 있다. 이후 그럼 M개의 질문을 받으면서 O(1)에 답을 출력해줄 수 있다. 이 때, (x1, y1)부터 (x2, y2)까지 합은 다음처럼 구할 수 있다.
(x1, y1)부터 (x2, y2)까지 합 = arr[x2][y2]-arr[x1-1][y2]-arr[x2][y1-1]+arr[x1-1][y1-1]

코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private static final BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private static StringTokenizer st;
private void setLine() throws Exception { st = new StringTokenizer(br.readLine()); }
private int ni() { return Integer.parseInt(st.nextToken()); }
private int get2dRangeSum(int[][] arr, int x1, int y1, int x2, int y2) {
return arr[x2][y2]-arr[x1-1][y2]-arr[x2][y1-1]+arr[x1-1][y1-1];
}
private void solution() throws Exception {
setLine();
int n = ni();
int m = ni();
int[][] arr = new int[n+1][n+1];
for(int i = 1; i <= n; i++) {
setLine();
for (int j = 1; j <= n; j++)
arr[i][j] = ni()+arr[i-1][j]+arr[i][j-1]-arr[i-1][j-1];
}
StringBuilder sb = new StringBuilder();
while(m-->0) {
setLine();
sb.append(get2dRangeSum(arr, ni(), ni(), ni(), ni())).append('\n');
}
System.out.print(sb);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 2559 - 수열 (boj java) (0) | 2022.05.27 |
|---|---|
| [자바] 백준 1671 - 상어의 저녁식사 (boj java) (0) | 2022.05.26 |
| [자바] 백준 21939 - 문제 추천 시스템 Version 1 (boj java) (0) | 2022.05.25 |
| [자바] 백준 18221 - 교수님 저는 취업할래요 (boj java) (0) | 2022.05.24 |
| [자바] 백준 23804 - 골뱅이 찍기 - ㄷ (boj java) (0) | 2022.05.23 |





댓글