목차
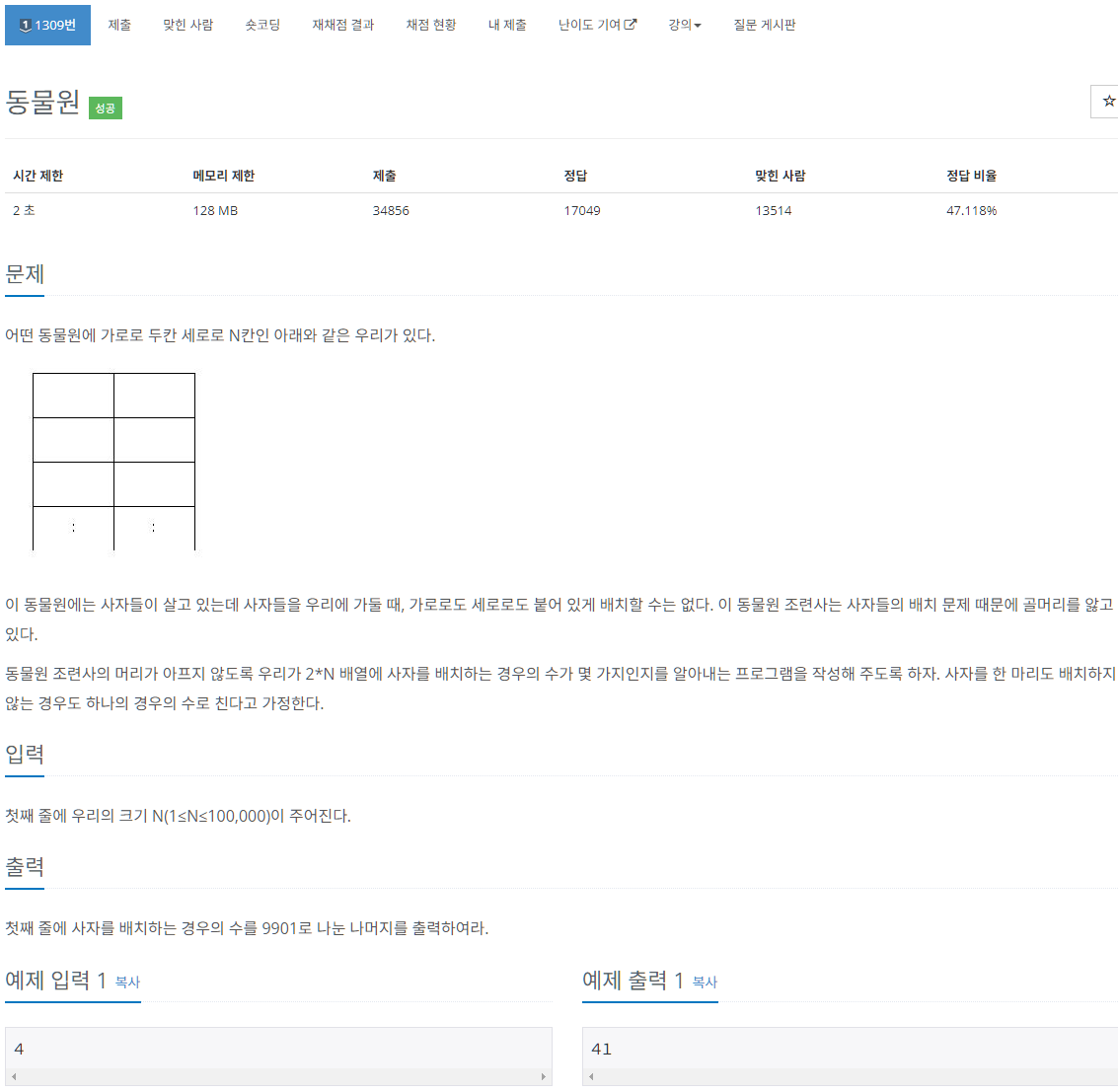
문제 : boj1309
필요 알고리즘
- DP (동적계획법, 다이나믹 프로그래밍)
- 기본적인 형태의 DP 문제이다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
Nx2 칸으로 동물원이 구성된다. N칸의 세로는 우선 생각하지 말고, 2칸인 가로칸의 존재 가능한 상태를 생각해보자.
다음과 같이 4가지 종류로 존재 가능하다. 다만 이 중 (d)는 가로로 붙어 있게 배치할 수 없다고 하였으므로 불가하여 (a)~(c)의 3가지만 이 문제에서 존재 가능하다.

그럼 이번엔 세로칸을 생각해보자. 상단의 칸의 상태에 따라, 아래칸에 (a)~(c)를 놓을 수 있는 경우는 다음과 같이 나타낼 수 있다. 세로칸에 붙어 있게 배치할 수 없다는 점을 생각하며 (a), (b), (c)의 형태를 세로로 한칸 더 배치한 셈이다.

이제 dp[x][y]를 정의해보자. dp[x][y]는 세로로 x번째 칸이 (a), (b), (c) 중 y형태일 경우의 수라고 정의해보자. x는 0부터 n까지의 값을 가지고, y는 0, 1, 2를 값으로 가지며 각각 (a), (b), (c) 형태를 의미한다.
그럼 위의 dp 정의를 가지고 그림을 점화식으로 만들면 다음과 같다.
dp[x][0] = dp[x-1][0] + dp[x-1][1] + dp[x-1][2]
dp[x][1] = dp[x-1][0] + dp[x-1][2]
dp[x][2] = dp[x-1][0] + dp[x-1][1]
-> 예를들어 위 그림에서 세로 2번째 칸에 파란색이 좌측에 있는 녀석은 dp[x][1] 이라 표현 가능하다. 세로 2번째 칸으로 진입 가능한 이전의 상태는 (a)와 (c)이고, 각각 dp[x-1][0]과 dp[x-1][2] 라고 표현할 수 있다. 따라서 dp[x][1] = dp[x-1][0] + dp[x-1][2] 이다.
이제 이 내용을 코드로 옮기면 된다!
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class Main {
private static BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 1 << 16);
private static final int MOD = 9901;
public static void main(String[] args) throws Exception {
new Main().solution();
}
public void solution() throws Exception {
int n = Integer.parseInt(br.readLine());
int[][] dp = new int[n+1][3];
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
dp[i][0] = dp[i-1][0] + dp[i-1][1] + dp[i-1][2];
dp[i][1] = dp[i-1][0] + dp[i-1][2];
dp[i][2] = dp[i-1][0] + dp[i-1][1];
for (int j = 0; j < 3; j++) dp[i][j]%=MOD;
}
System.out.println((dp[n][0]+dp[n][1]+dp[n][2])%MOD);
}
}
'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 3142 - 즐거운 삶을 위한 노력 (java) (0) | 2024.02.23 |
|---|---|
| [자바] 백준 3089 - 네잎 클로버를 찾아서 (java) (0) | 2024.02.22 |
| [자바] 백준 7588 - Amicable (java) (0) | 2024.02.19 |
| [자바] 백준 16400 - 소수 화폐 (java) (0) | 2023.12.15 |
| [자바] 백준 13565 - 침투 (java) (0) | 2023.12.15 |





댓글