목차
문제 : boj20500

필요 알고리즘
- 동적 계획법 (DP), 정수론
- 정수론 특히 나머지 연산의 성질에 대해 알아야 하고, 효율적으로 풀기 위해 DP가 필요하다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
아래와 같이 자리수를 늘려나가 만들어지는 N자리 양의 정수 중 15의 배수가 몇 개인지 구하는 문제이다.
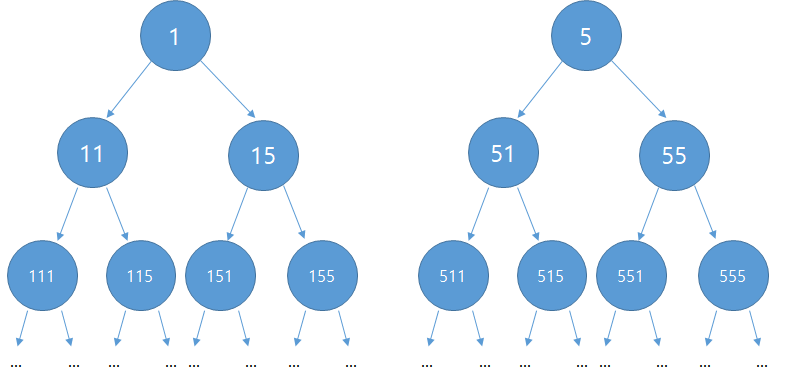
당연하게도 1과 5로 이루어진 N자리 수는 2^N 개나 된다. 2^1515개의 정수는 천문학적인 수치이므로 brute force로 직접 확인해볼 순 없다.
이 때 어떠한 숫자 X의 뒤에 1과 5를 한 자리 더 더하는 과정은
X*10+1과 X*10+5 라고 볼 수 있다. 그리고 우리가 알아야 하는건 N자리 수가 실제로 어떤건지가 아니라, 15의 배수인지만 알면 된다. 이 때 나머지 연산에는 다음과 같은 공식이 성립한다. 즉, X*10+1을 하는 과정에서 저 X는 실제 N-1자리수의 값이 아니라, 그냥 15로 나눈 나머지여도 X*10+1이 15로 나누어 떨어지는지 확인하는데 문제가 없다는 얘기이다.
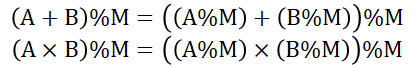
그렇다면, 15의 나머지는 총 15개(0~14) 뿐이므로 이제 우린 나머지의 종류 15가지에 대해서만 각각 N-1 자리수에서 몇 번이나 나왔는지만 알고 있으면 된다.
dp[a][b]를 'a자리수 양의 정수에서 15로 나눈 나머지가 b인 경우의 수' 라고 해보자.
예를들어 N=3인 경우 양의 정수는 111, 115, 151, 155, 511, 515, 551, 555가 존재한다.
이 때 dp[3]은 다음과 같다.
[1, 2, 0, 0, 0, 2, 1, 0, 0, 0, 1, 1, 0, 0, 0]
만약 N=3인 경우 dp[3][0] (=3자리 수에서 15로 나눈 나머지가 0인 경우의 수)인 1이 답이 된다.
그리고 정답또한 1,000,000,007로 나눈 나머지를 출력해야 하는데, 같은 원리로 매번 저 수로 나눈 나머지만 dp 배열에 유지해줘도 정답을 구하는데 문제가 없다.
dp[1][1] = dp[1][5] = 1; // 1자리수는 1과 5 두 가지 이다. 이 경우에 대해 초기화 해준다.
for (int i = 2; i <= n; i++) { // 한자리씩 늘려가면서
for (int bf = 0; bf <= 14; bf++) { // dp의 이전 나머지에다가
int tmp = bf*10+1; // 숫자 1을 뒤에 붙인다.
tmp%=15; // 15로 나눈 나머지만 유지할꺼다.
dp[i][tmp] += dp[i-1][bf]; // dp에 경우의 수를 더해준다.
dp[i][tmp] %= MOD; // 정답 역시 1,000,000,007로 나눈 나머지만 유지해준다.
tmp = bf*10+5; // 마찬가지로 숫자 5를 뒤에 붙인다.
tmp%=15;
dp[i][tmp] += dp[i-1][bf];
dp[i][tmp] %= MOD;
}
}
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 1 << 16);
private static final int MOD = 1000000007;
public static void main(String[] args) throws Exception {
new Main().solution();
}
public void solution() throws Exception {
int n = Integer.parseInt(br.readLine());
long[][] dp = new long[n+1][15];
dp[1][1] = dp[1][5] = 1;
for (int i = 2; i <= n; i++) {
for (int bf = 0; bf <= 14; bf++) {
int tmp = bf*10+1;
tmp%=15;
dp[i][tmp] += dp[i-1][bf];
dp[i][tmp] %= MOD;
tmp = bf*10+5;
tmp%=15;
dp[i][tmp] += dp[i-1][bf];
dp[i][tmp] %= MOD;
}
}
System.out.println(dp[n][0]);
}
}
'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 2418 - 단어 격자 (java) (0) | 2023.12.08 |
|---|---|
| [자바] 백준 30646 -최대 합 순서쌍의 개수(java) (0) | 2023.12.06 |
| [자바] 백준 1612 - 가지고 노는 1 (java) (0) | 2023.12.04 |
| [자바] 백준 1584 - 게임 (java) (0) | 2023.12.01 |
| [자바] 백준 10448 - 유레카 이론 (java) (0) | 2023.12.01 |





댓글