문제 : boj20955

필요 알고리즘 개념
- 트리
- 트리의 특징에 대해 알고 있어야 이 문제를 풀 수 있다.
- 분리 집합 (disjoint set) 혹은 유니온 파인드 (union-find)
- 분리 집합 알고리즘인 유니온 파인드를 알고 있으면 간단하게 이 문제를 풀 수 있다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
이 문제에서는 정점의 개수가 주어지고(N), M개의 간선 정보가 주어진다. 그럼 다음의 입력값을 생각해보자.
7 8
1 2
2 3
1 3
4 5
4 6
4 7
5 6
6 7
주어진 정보를 그래프로 그려보면 다음과 같다.

이 그래프의 모든 정점이 하나의 트리가 되기 위해서는 우선 사이클이 발생한 곳을 전부 끊어줘야 한다. 즉, 사이클이 발생하지 않도록 적절하게 간선을 끊어줘야 한다.
서로 탐색이 가능한 정점들을 하나의 그룹으로 생각해보자. 그럼 이 경우엔 1-2-3 그룹과, 4-5-6-7이 있다. 이 그룹이 변경되지 않으면서(즉, 탐색가능하던게 불가하지 않게 하면서) 사이클이 발생하지 않도록 간선을 끊는 여러 방법 중 2가지는 다음과 같다. 둘다 총 3개를 끊었으며, 정확히 3개를 끊어야만 탐색 가능한게 변경되지 않으면서 사이클을 제거할 수 있다.
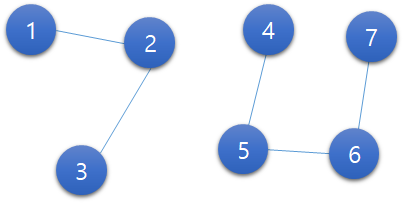

다음으로 모든 정점이 하나의 트리로 나타나야 하므로, 그룹끼리도 아무곳이나 한 곳을 연결해줘야 한다. 예를들어 아래와 같이 연결해주면 된다(많은 방법들 중 하나이다.).
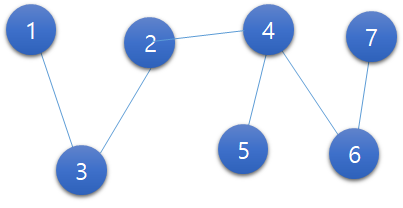
즉 정리하면, 이 문제에서 답으로 출력해야 하는 최소 연산 횟수는
[ 각 그룹(탐색 가능한 정점들의 집합)에 사이클이 발생하지 않도록 간선 끊은 횟수 ] + [ 그룹의 수 - 1 ] 이 될 것이다(그룹의 수가 X개일 때 모든 그룹을 연결하기 위해서는 간선 X-1개가 추가되어야 하므로)
그럼 머리론 이제 대강 알겠는데, 이걸 어떻게 구현해야 할지 막막할 것이다. 일단 뭐 그룹 관련 문제라면 일단 분리 집합 알고리즘으로 생각해보면 좋다. 아주 자주 쓰이고 응용되어 여러 알고리즘에 사용할 수 있는 녀석으로 혹시 모르는 개념이라면 꼭 검색해서 익혀두자.
우선 각 그룹에서 사이클을 어떻게 찾을지 확인해보자. 단순히 분리 집합 개념만 알고 있었다면, 이걸로 어떻게 사이클이 발생하는지 체크가 가능할지 궁금할 것이다. 혹시 Kruskal Algorithm으로 MST(Minimum Spanning Tree)를 찾는 문제를 풀어봤다면 한번 써봤을 수도 있는데, 사실 union으로 각 정점을 합치던 도중에 이미 동일한 그룹에 속한 정점이 합쳐진다면 사이클이 생기는 경우가 된다. 따라서 union에서 동일한 그룹인 경우를 카운팅해주면 된다. 코드에서는 'if (!union(u, v)) cnt++;' 부분이 그 역할을 한다(union 함수에서 서로 동일한 그룹인 경우, false를 리턴하도록 해뒀다.).
다음으로 그룹의 개수는 union-find 알고리즘을 알고있다면 간단히 알 수 있다. 부모 정점의 개수를 세주면 된다. 내 경우엔 parents[] 배열에 부모 정점일 경우 음수값으로 grade(몇 개의 자식을 포함하는지)를 기입해뒀다. 따라서 코드로는 'if (parents[i]<0) cnt++;'가 된다. 구현방식에 따라 다를 수 있으니 코드를 참고해서 자신이 짠 분리 집합 로직에 맞도록 짜보자.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
private int[] parents;
private void init(int n) {
parents = new int[n+1];
Arrays.fill(parents, -1);
}
private int find(int a) {
if (parents[a] < 0) return a;
return parents[a] = find(parents[a]);
}
private boolean union(int a, int b) {
a = find(a);
b = find(b);
if (a == b) return false;
int h = parents[a]<parents[b]?a:b;
int l = parents[a]<parents[b]?b:a;
parents[h]+=parents[l];
parents[l] = h;
return true;
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
init(n);
int cnt = 0;
while (m-->0) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
if (!union(u, v)) cnt++;
}
for (int i = 1; i <= n; i++) {
if (parents[i]<0) cnt++;
}
System.out.println(--cnt);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 10830 - 행렬 제곱 (java) (0) | 2022.08.02 |
|---|---|
| [자바] 백준 1148 - 단어 만들기 (java) (0) | 2022.08.02 |
| [자바] 백준 23303 - 이 문제는 D2 입니다. (java) (0) | 2022.07.30 |
| [자바] 백준 25314 - 코딩은 체육과목 입니다 (java) (0) | 2022.07.30 |
| [자바] 백준 21918 - 전구 (java) (0) | 2022.07.28 |





댓글