문제 : boj2166
필요 알고리즘 개념
- 기하학
- 신발끈 공식을 사용해 풀 수 있는 문제이다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
솔브닥 그래프에 기하학이 폭-삭 상태인데, 왠지 동그란게 이쁠 것 같으니 기하학을 공부해보기로 했다.
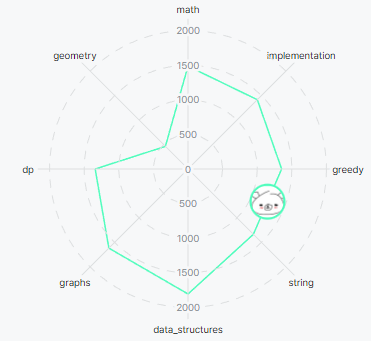
이 문제는 기하학의 사칙연산이라 불리는 CCW를 다양한 블로그 보면서 공부하고 있던 중에 만난 신발끈 공식으로 풀 수 있는 문제였다. 이하 노션에 개인 공부용으로 정리중인 벡터의 외적 및 CCW 내용이다.
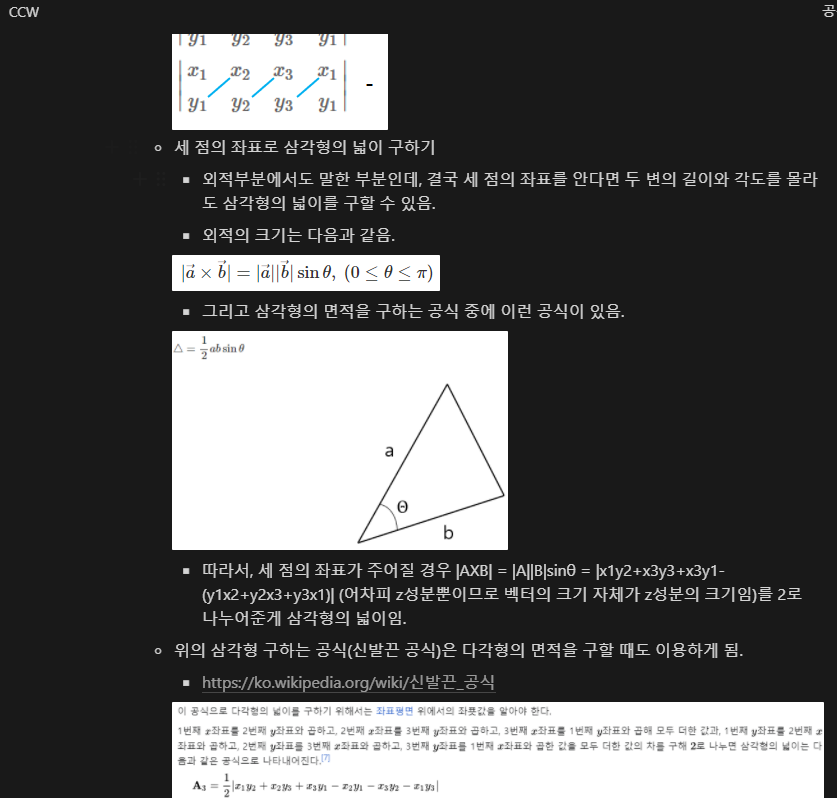
아무튼 그러니 풀이는 그냥 공식만 잘 쓰면 되므로, 신발끈 공식 위키 링크로 대신한다. int형으로는 오버플로우가 발생하는 부분에 주의해야 한다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[][] arr = new int[n+1][2];
for (int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
arr[i][0] = Integer.parseInt(st.nextToken());
arr[i][1] = Integer.parseInt(st.nextToken());
}
arr[n][0] = arr[0][0];
arr[n][1] = arr[0][1];
long sum = 0;
for (int i = 0; i < n; i++) {
sum += 1l*arr[i][0]*arr[i+1][1] - 1l*arr[i+1][0]*arr[i][1];
}
sum = Math.abs(sum);
System.out.printf("%.1f", 1d*sum/2);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 1990 - 소수인팰린드롬 (java) (0) | 2022.11.10 |
|---|---|
| [자바] 백준 6322 - 직각 삼각형의 두 변 (java) (0) | 2022.11.10 |
| [자바] 백준 17502 - 클레어와 팰린드롬 (java) (0) | 2022.11.07 |
| [자바] 백준 3724 - 표 (java) (0) | 2022.11.07 |
| [자바] 백준 13985 - Equality (java) (0) | 2022.11.07 |





댓글