목차
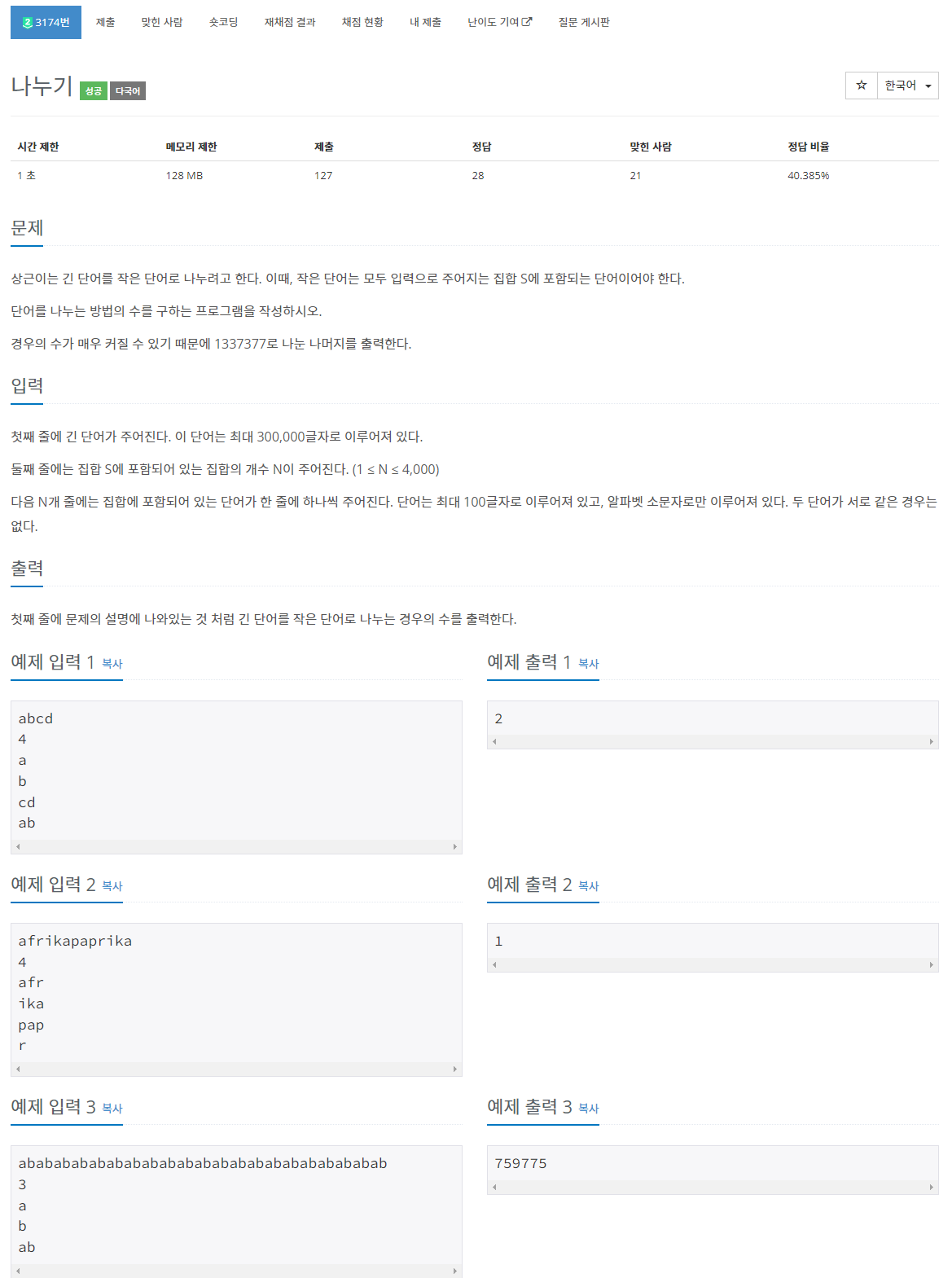
문제 : boj3174
필요 알고리즘
- 동적 계획법(다이나믹 프로그래밍, DP), 트라이(Trie)
- DP를 기본으로 깔고, DP 진행을 효율적으로 하기 위해 트라이를 사용하면 좋은 문제이다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
1. 우선 경우의 수를 어떻게 구할 수 있는지부터 생각해보자.
예제 입력 1을 보자.
abcd
4
a
b
cd
ababcd 라는 문자열에서 우선 첫 번째 문자인 a부터 시작해보자.
a부터 시작해 abcd에 포함되는 단어는 'a'와 'ab'이다.
그 다음 abcd에서 b부터 보면, 'b'만 포함시킬 수 있다.
abcd에서 c부터 보면 'cd'만 가능하다.
abcd에서 d부터 보면 가능한게 없다.
이걸 dp라는 배열로 한번 표현해보자. dp[i]는 abcd의 i번째 문자까지 표현하는 경우의 수를 나타낸다. 그렇다면 아래처럼 표현해볼 수 있다. abcd 에서는 'a'와 'ab'가 가능하므로 dp[1]과 dp[2]를 각각 1씩 증가시킨다. abcd 에서는 abcd의 처음 'a'를 표현 가능한 경우의 수가 1개이고, 그 이후로 'b'를 붙일 수 있으므로 dp[2] += dp[1]을 해준다. +1이 아니라 dp[1]을 해줬다는 점에 주의하자. abcd 에서는 abcd에서 처음 'ab'까지 표현 가능한 경우의 수인 2에서, 'cd'를 뒤에 붙이는게 가능하므로 dp[4] += dp[2]를 해준다. abcd 는 애초에 abcd에서 처음 'abc'를 표현 가능 가능한 경우의 수가 0 이므로 무시하면 된다.

2. 위 설명이 감이 잘 안올 수 있다.
그러니까, 만약 '1'에서 봤던 예제가 다음과 같다고 해보자. 'd'가 단어로 추가됬다.
abcd
5
a
b
cd
ab
d이러면 abcd 를 보고 있는 경우에 'd'를 바로 표현 가능하니 경우의 수가 달라질까?
달라지지 않는다. 애초에 abcd에서 처음 'abc'를 표현 가능한 경우의 수가 0 이므로, 그 뒤에 'd'를 붙일 수 없는 것이다. 이걸 이해해야 풀 수 있다.
그리고 dp[4] += dp[2] 이런식으로 점화식을 잡은게 잘 이해안될 수 있다. 말로 표현해보면 이해할만 할 것 같다. "'abcd'에서 처음 'ab'에다가 'cd'를 붙일 수 있으므로, 'abcd'를 표현하는 경우의 수(dp[4])는 'ab'를 표현하는 경우의 수(dp[2])에다가 'cd'를 붙이는 한 가지 경우가 생긴게 되는 것이다."
3. 사실 여기까진 기본적인 DP 문제다.
문자열 문제가 아니라 쉽게 처리가 가능했거나, 문자열 길이가 좀 작았다면 사실 골드정도로 티어가 책정됬을 것 같은 무난한 DP 문제이다.
문제는 상당히 길이가 긴 문자열이 포함된 문제라는 점인데, 이 부분을 처리하기 위해 내 경우엔 Trie를 사용했다.
미리 n개의 단어들을 트라이에 등록한 뒤, 긴 문자열의 첫 번째 문자부터 확인하면서 각 문자부터 시작해 트라이로 진행 가능한 부분까지 진행하면서 dp 배열을 갱신하는 방식으로 구현했다.
private void solution() throws Exception {
String str = br.readLine();
TrieRoot trie = setupTrie();
int len = str.length();
int[] dp = new int[len+1];
dp[0] = 1; // 초기값을 1로 잡아줘야 편하다. 그래서 dp[i]에서 i를 0부터 시작 안하고 1부터 했다.
for (int i = 1; i <= len; i++) {
int base = dp[i-1]; // base = 직전 문자까지 표현 가능한 경우의 수
if (base == 0) continue; // 직전 문자까지 표현 가능한 경우가 0이면 무시하면 된다.('2')
Node iter = trie.root.peek(str.charAt(i-1));
int pt = i; // 긴 문자열의 i번째 문자부터 pt를 증가시키며 살펴볼꺼다.
while (true) {
if (iter == null) break; // 트라이에서 더이상 진행 불가하면 멈춘다.
if (iter.isWordExist()) { // n개의 단어 중 맞는 단어를 발견하면
dp[pt] += base; // 얘기한대로 경우의 수를 base 만큼 증가시키면 된다.
dp[pt] %= MOD; // 나머지의 법칙에 의해 매번 나머지를 계산해둬도 답은 동일하다.
}
if (pt == len) break;
iter = iter.peek(str.charAt(pt++)); // pt를 증가시키며 다음 문자로 진행!
}
}
System.out.println(dp[len]); // 최종 답은 dp['긴 문자열의 길이'] 가 된다.
}
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private static final int MOD = 1337377;
public static void main(String[] args) throws Exception {
new Main().solution();
}
private void solution() throws Exception {
String str = br.readLine();
TrieRoot trie = setupTrie();
int len = str.length();
int[] dp = new int[len+1];
dp[0] = 1;
for (int i = 1; i <= len; i++) {
int base = dp[i-1];
if (base == 0) continue;
Node iter = trie.root.peek(str.charAt(i-1));
int pt = i;
while (true) {
if (iter == null) break;
if (iter.isWordExist()) {
dp[pt] += base;
dp[pt] %= MOD;
}
if (pt == len) break;
iter = iter.peek(str.charAt(pt++));
}
}
System.out.println(dp[len]);
}
private TrieRoot setupTrie() throws Exception {
TrieRoot trie = new TrieRoot();
int n = Integer.parseInt(br.readLine());
while (n-->0) {
trie.add(br.readLine());
}
return trie;
}
}
class TrieRoot {
Node root;
public TrieRoot() {
root = Node.root();
}
public void add(String s) {
Node iter = root;
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
iter = iter.retrieveChild(c);
}
iter.endOfWord();
}
}
class Node {
private boolean isWordExist;
private Node[] child;
private Node() {
isWordExist = false;
child = new Node['z'-'a'+1];
}
public static Node root() {
return new Node();
}
public void endOfWord() {
isWordExist = true;
}
public Node retrieveChild(char c) {
int idx = c - 'a';
if (child[idx] == null) {
child[idx] = new Node();
}
return peek(c);
}
public Node peek(char c) {
int idx = c - 'a';
return child[idx];
}
public boolean isWordExist() {
return isWordExist;
}
}
'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 17365 - 별다줄 (java) (0) | 2023.07.10 |
|---|---|
| [자바] 백준 15681 - 트리와 쿼리 (java) (0) | 2023.07.10 |
| [자바] 백준 9202 - Boggle (java) (0) | 2023.06.27 |
| 백준 1002 자바 - 터렛 (BOJ 1002 JAVA) (0) | 2023.06.22 |
| [자바] 백준 12893 - 적의 적 (java) (0) | 2023.06.18 |





댓글