목차
※ References에 적어둔 여러 글을 보며 공부한걸 나중에 까먹지 않기 위해 제가 이해한 내용을 제가 이해한 방식으로 필기 해두는식으로 적은 글 입니다. 그러니 개념을 더 제대로 살펴보시려면 References의 잘써둔 글들을 참고해주세요. 그나마 이 글의 장점이라면 제가 수학에 매우 약하기 떄문에 제가 이해한 방식으로 적어두면 다른 분들은 훨씬 금방 이해하심. 틀린거 있으면 알려주세요!
※ 용어 : 이하 글에서 구간합은 'A부터 B까지의 합', 누적합은 '1부터 N까지의 합', 누적합 알고리즘은 prefix sum 알고리즘을 뜻합니다.
※ 기본적으로 중간 중간에 있는 코드 예시는 c++, java 모두 통용되는 코드로 작성했습니다. 어차피 구현이 간단한 부분들이므로 어떤 언어를 사용하던지 이해하기 무리가 없을 것이라 생각합니다. 알고리즘 예시에서는 전체 코드를 예시로 들어두었으므로, 이 때는 자바와 c++ 코드를 둘 다 작성하여 넣어두었습니다. 마찬가지로 펜윅 트리 자체가 구현이 간단한게 큰 장점으로 다른 언어 사용자라도 이해하는데 무리는 없으시리라 생각됩니다.
서론
펜윅 트리란?
데이터 압축에서 효율성 향상을 위해 Fenwick, Peter M이 1994년에 논문으로 발표한 자료 구조이다.
| "A new method (the 'binary indexed tree') is presented for maintaining the cumulative frequencies which are needed to support dynamic arithmetic data compression."1 |
논문에서 제시된 기본 구조에서 '단일 값 변경(point update) + 구간에 대한 값 획득(range query)'이 가능하고, 응용으로 '구간에대한 값 변경(range update) + 단일 값 획득(point query)', '구간에 대한 값 변경(range update) + 구간에 대한 값 획득(range query)'이 가능해서 PS(Problem solving)에서 범위 쿼리 문제에서 심심치 않게 사용된다.
저자인 펜윅이 제시한건 binary indexed tree라는 이름이라서 해당 이름 그대로와 약어인 BIT로도 불리고, 저자가 Fenwick 이므로 Fenwick tree 라고도 불린다(다익스트라가 사람 이름 그대로인 것 처럼). 이 글에서는 이후 '펜윅 트리'라고 호칭한다.
알고리즘 문제풀이(Problem Solving, 이하 PS)에서는 주로 세그먼트 트리(segment tree)로 풀 수 있는 문제 중 일부 문제를 좀 더 적은 메모리와 쉬운 코드로 풀 수 있는 알고리즘으로써 알려져 있다. 개인적으로는 세그먼트 트리 보다는 누적합(prefix sum, 이하 누적합) 알고리즘에서 펜윅트리로 개념을 확장하는것이 더 이해하기 좋다고 본다(누적합을 계산해서 구간합을 구한다는 점, 2D 구간합에 대한 개념이 비슷한 점 등). 이 글 또한 누적합 알고리즘 기반에서 개념을 확장하며 작성했기 때문에 누적합 알고리즘에 대해 모른다면 누적합 알고리즘 글부터 먼저 보고 이 글을 보는걸 추천한다.
펜윅 트리 사용 이유
누적합 알고리즘의 경우 1번째부터 N번째 까지의 합 정보를 이용해 구간합(A번째부터 B번째 까지의 합)을 O(1)로 구할 수 있다(1부터 B까지의 합에서 1부터 A-1까지의 합을 빼주면 A부터 B까지의 합이 된다). 하지만 만약 X(1<=X<=N)번째 값이 변경될 경우엔 어떻게 될까? X번째부터 N번째까지 계산해둔 누적합을 모두 변경해줘야 함이 당연하므로 O(N)이 필요하다.

펜윅 트리의 경우 누적합 알고리즘과 동일하게 1번째부터 N번째 까지의 합을 효율적으로 저장하기 위한 자료구조이다. 따라서 누적합 알고리즘과 마찬가지의 방식으로 1부터 A-1까지의 합과, 1부터 B까지의 합 정보를 가지고 A부터 B까지의 구간합을 구할수 있다. 다만 누적합 알고리즘과는 저장하는 방식이 달라 O(logN)으로(밑이 2인 로그) 구간합을 구할 수 있다. 그럼 O(1)인 누적합 알고리즘보다 비효율적인데 왜 쓰냐면, 대신 중간에 값이 변경되는걸 누적합 알고리즘보다 빠르게 O(logN)으로 처리할 수 있다.

즉, 구간합을 구해야 하는데 처음에만 데이터가 주어지고 이후 값이 변경되지 않는다면 누적합 알고리즘을 쓰는게 효율적이고, 중간에 값이 변경되어야 한다면 펜윅 트리를 쓰는게 효율적이다.
물론 위의 경우에 가장 많이 사용되는건 세그먼트 트리(segment tree)이다. 세그먼트 트리도 마찬가지로(스플레이 트리도 마찬가지) 구간합을 O(logN)에 구할 수 있고, 중간에 값이 변경되는 것도 O(logN)으로 처리할 수 있다. 그럼 굳이 펜윅 트리를 알아야 할까? 세그먼트 트리에 비해 펜윅 트리의 장점은 메모리를 더 적게쓰고(단, PS에서는 거의 모든 경우에 세그먼트 대신 펜윅을 써야만 통과될 정도로 빡빡하게 메모리 제한을 걸어두지 않는 편이다. 그리고 단순히 메모리만 보면 제곱근 분할법(sqrt decompositon)이 더 응용력이 높고 메모리도 적게든다. 대신 시간복잡도가 증가함.), 약간이지만 속도도 빠르다. 제일 중요한건 코드가 간단하다는 점이다. 아래 코드는 동일한 문제를 세그먼트 트리와 펜윅 트리로 푼 경우인데(자바지만 다른 언어 사용자라도 대충 길이만 봐주세요!), 펜윅 트리쪽이 코드가 더 간결함을 볼 수 있다. 거기에 세그먼트 트리에 lazy propagation 개념까지 더해야 풀리는 일부 문제들도 펜윅 트리를 응용하면 더 간결하고 상대적으로 적은 지식으로 풀 수 있다.
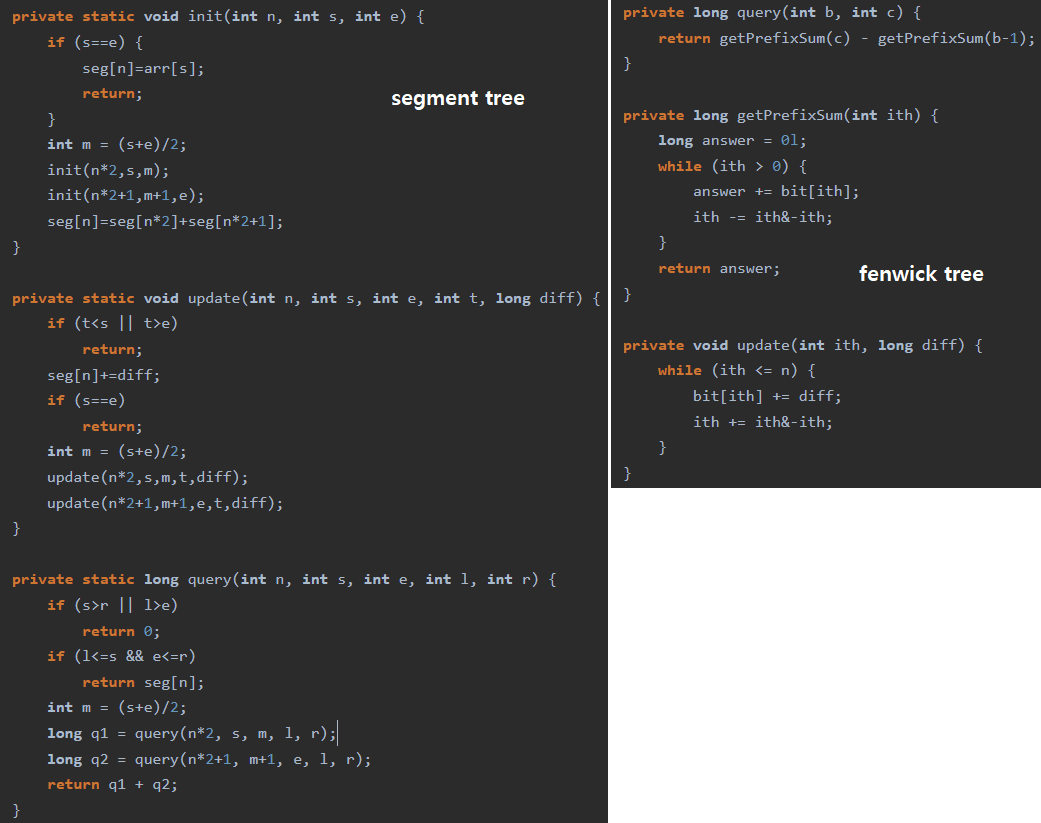
한 문제에 대해 세그먼트 트리, 0베이스(용어에 대해서는 아래쪽에 읽다보면 나온다) 펜윅 트리, 1베이스 펜윅 트리, 논문에서 제시한 방법대로 구현했을 때의 메모리와 시간 차이를 봐본 것이다.

이건 또 다른 문제에 대해 제곱근 분할법(sqrt decomposition)과의 시간차이를 본 것이다.

펜윅 트리의 한계
일반적으로 구간합을 계산하는 용도 이외에는 사용이 어렵다. 구간합 이외의 대부분의 구간 쿼리에 대해 세그먼트 트리가 훨씬 더 활용성이 높다. 예를들어 해당 구간의 최대 최소값(RMQ, range max/min query) 질의에 대해 펜윅트리로는 뒤로갈수록 값이 커지거나(최대값 구할 때), 작아지는(최소값 구할 때) 데이터에 대해서만, 그것도 구간 쿼리가 [1, X]와 같이 들어와야만 답변이 가능하다. 펜윅 트리 2개를 사용해 좀 더 개선할 수는 있으나 마찬가지로 제한적이고 애초에 그럼 코드가 간단하다는 장점이 없어질 것이다. 즉, 펜윅 트리로 할 수 있는건 세그먼트 트리나 스플레이 트리 등으로 구현 가능하지만 그 반대는 항상 성립하는게 아니다.
기본 : 펜윅 트리 (point update + range query)
시작하기 전에
내 경우엔 인덱스 0번을 사용하지 않고, 인덱스 1번부터 사용하는 방식을 선택했다. 즉, N개짜리 배열이라면 arr[N]로 선언하고 인덱스 0~N-1을 쓰는(이하 0베이스)게 아니라, arr[N+1]로 선언하고 1~N을 사용하는 방식(이하 1베이스)이다. 그 이유는 이하 0베이스와 1베이스로 동일한 코드를 구현한 코드를 보면 알 수 있다. 1베이스로 짠 펜윅트리가 더 이해하기도 쉽고 보기도 좋다('ith -=', 'ith +='로 +와 -만 달라졌다). 0베이스로 펜윅트리를 익히고 싶다면 Reference 2번에 자세히 구현이 나와있다.

근데 애초에 원본 논문에서도 1베이스로 구현되어있다. 이하 논문의 일부인데, 총 15개의 데이터에 대해 16개짜리 배열로 표현해뒀다(값이 들어가 있는게 저 빗금쳐둔 부분들이다). 그림에 내가 추가로 그려둔 16번째는 16개의 데이터를 17개짜리 배열로 표현할 경우 16번째 값은 모든 데이터의 합임을 나타낸다(아직은 뭔소린지 몰라도 상관없다).

구현을 설명하기 전에 얘기할게, 펜윅 트리 구현에서 가장 중요한 비트연산 하나를 먼저 설명하겠다. 어떠한 정수를 2진수로 봤을 때 가장 오른쪽 '1' 비트만 남긴 값을 계산하는 비트연산을 알아야 한다. 즉, 2진수로 11010을 00010으로 변경하는 방법을 알아야 한다. 이건 정수 X에 대해 (X&-X) 를 해주면 된다(&은 bitwise AND). 알다시피 컴퓨터에서 음수는 해당 수의 모든 비트를 반전시킨 1의 보수에 +1을 한 2의 보수로 표현한다. 따라서 X&-X를 해주게 되면 다음과 같이 X의 가장 오른쪽 '1' 비트만 남은 값이 된다.

펜윅 트리의 데이터 저장 방식
펜윅 트리의 기본 아이디어는 정수를 2의 거듭제곱의 합으로 나타낼 수 있다는 점이다. 컴퓨터는 2진법을 사용하고 있고, 알다시피 정수를 표현하는 int, long 모두 2의 거듭제곱의 합으로 정수를 표현하고 있다.
| "The basic idea is that, just as an integer is the sum of appropriate powers of two, so can a cumulative frequency be represented as the appropriate sum of sets of cumulative 'subfrequencies'."1 |
16개의 데이터가 있는 경우를 생각해보자. 펜윅 트리의 저장 방식에서 중요한건 각 인덱스를 2진수로 나타냈을 때, 가장 오른쪽에 존재하는 '1'이다. A행에 각 인덱스값을 2진수로 나타내고, 가장 오른쪽에 있는 '1'을 빨간색으로 나타냈다. 다음으로 B행에 가장 오른쪽 '1'을 제외한 나머지를 모두 0으로 변경한 2진수를 적어두었다(B[idx] = A[idx]&-A[idx]). C행은 B행의 값을 다시 10진수로 변경한 값이다.

펜윅 트리에서 데이터를 저장하는 방식은 해당 idx 위치에 그 이하 C[idx]개 만큼의 데이터 합을 담아두는 것이다(즉, [idx-C[idx]+1, idx] 범위의 합.). D행에 C[idx]에 따라 인덱스 몇번부터 몇번까지의 구간합을 저장하고 있는지 표현해두었다. 예를들어 1번 인덱스의 경우 C[1] = 1 이므로, [1, 1] 범위의 합을 담는다. 8번 인덱스의 경우 C[8] = 8 이므로 [1, 8]로 1번 인덱스부터 8번 인덱스 까지의 합을 담아둔다.
arr행에 펜윅 트리를 사용해 구간합을 구하고자 하는 데이터 값을 담아두었다(예를들어 arr[4] = 2). 그리고 bit행에 D[idx]에 해당하는 범위의 합을 저장해 두었다. 예를들어 D[12]가 [9,12]이므로, bit[12] = arr[9]+arr[10]+arr[11]+arr[12] = 1+0+3+0 = 4 이다. 저 bit 배열이 원본 데이터 arr[]에 대해 펜윅트리 자료구조를 만든 것에 해당한다.

bit배열의 각 idx가 가지고 있는 구간합을 시각적으로 표현해보면 다음과 같다.

구현 1 : 값 변경(point update) 및 초기 데이터 삽입 방법
초기 데이터 삽입 방법을 알아보기 전에, 값 변경을 어떻게 O(logN)에 할 수 있는지 확인해보자. 우선 bit[idx]에 각각 어떠한 범위의 구간합이 들어가는지 이미 지정했으므로, 특정 X 인덱스의 값이 변경되었을 경우 다음과 같이 해당 구간에 포함되는 부분을 모두 변경해주면 된다. 예를들어 arr[11]의 값을 변경할 경우 bit[11], bit[12], bit[16] 을 변경해주면 된다. 이 때 변경이라는 말은 'arr[11]이 변경된 값 - 기존 arr[11]' 값을 bit[11], bit[12], bit[16]에 더해주는걸 의미한다(해당 차이만큼 변경된 것이므로).
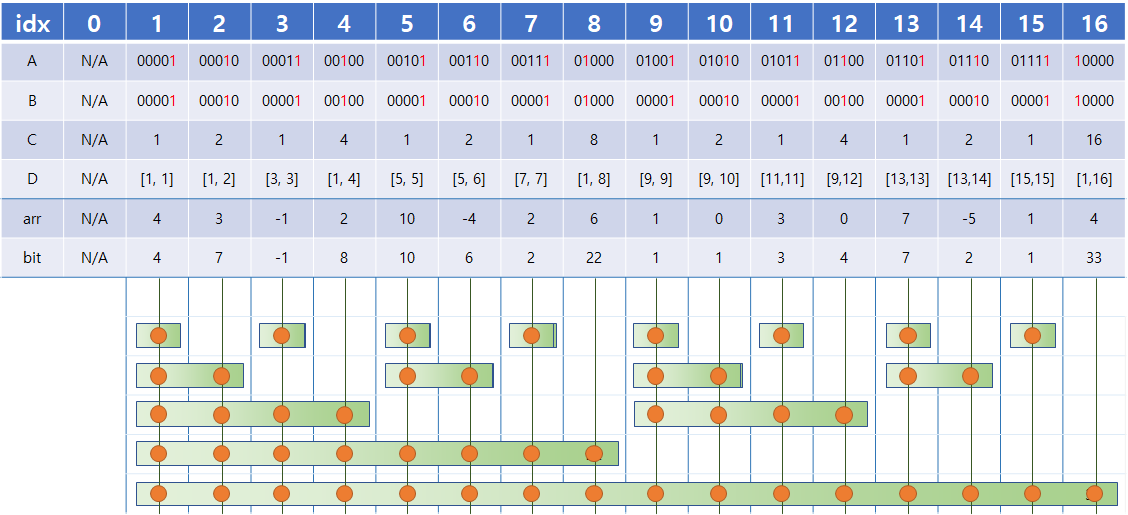
이걸 어떻게 구현할 수 있을까? arr[11]이 변경될 때 변경되는 11, 12, 16 인덱스의 A행을 보면 01011 -> 01100 -> 10000 순서로 변경된다. 이건 매번 맨 오른쪽 '1'에 +1을 해준 것과 같다(= 매번 맨 오른쪽 '1'만 남긴 것을 원래 값에 더해줌). 즉 A행의 값에 B행의 값을 더해주면 다음 idx가 나오는 방식이다. 당연히 idx가 N(위 예시에선 N=16)을 넘어갈때까지 진행해주면 된다.
1. 01011 + 00001 = 01100
2. 01100 + 00100 = 10000
3. 10000 + 10000 = 100000 에서 N값을 넘어가므로(2진수 100000은 10진수로 32) 종료.
하나 더 보면 arr[3]이 변경될 때 bit[3], bit[4], bit[8], bit[16]이 변경되어야 한다.
1. 00011 + 00001 = 00100 (인덱스 4)
2. 00100 + 00100 = 01000 (인덱스 8)
3. 01000 + 01000 = 10000 (인덱스 16)
4. 10000 + 10000 = 100000 (인덱스 32) 에서 N값을 넘어가므로 종료.
논문에 나온대로 구현을 하면 된다. 저기서 Val은 변경된 값(5에서 8로 변경 시 8-5해서 3이 Val)을 뜻한다.

코드로 다음과 같이 구현할 수 있다. diff는 'arr[x]이 변경된 값 - 기존 arr[x]값'을 의미한다. 즉, 문제에서 '[A, B] 범위를 X만큼 증가해라' 라면 diff를 따로 계산하지 않고 그대로 쓰면 된다. 하지만 '[A, B] 범위를 X로 변경한다.'라고 한다면 따로 변경된 수치를 당연히 계산해줘야 한다. 그리고 그런 경우라면 이후에 다시 x 위치가 변경될 수 있으므로 이후 diff를 계산하기 위해 arr[x]도 변경된 값으로 변경해줘야 한다. 이하 코드는 후자를 기준으로 짠 코드이다.
void update(int ith, int val) {
int diff = val - arr[ith];
arr[ith] = val;
while (ith <= n) {
bit[ith] += diff;
ith += ith&-ith;
}
}
...
while(값 변경 쿼리마다) {
int idx = [변경할 인덱스];
int changeTo = [변경할 값];
update(idx, changeTo);
}
물론 update 함수를 호출하기 전에 미리 변화한 값을 구해두고, diff를 인자로 받아도 된다. 이건 구현 방식의 차이이다.
void update(int ith, int diff) {
while (ith <= n) {
bit[ith] += diff;
ith += ith&-ith;
}
}
...
while (값 변경 쿼리마다) {
int idx = [변경할 인덱스];
int changeTo = [변경할 값];
int diff = changeTo - arr[idx];
arr[idx] = changeTo;
update(idx, diff);
}
그리고 어차피 구간합에 대해 arr[x]의 값은 [x, x]의 구간합과 동일하다. 따라서 원본 배열 자체를 안쓰고도 구현할 수 있다. getPrefixSum(x)는 [1,x]의 구간합이다. 이 바로 다음 '구간합 획득 query'에서 어떻게 구현하는지 얘기할 것이니 그냥 그런 함수라고만 생각해주면 된다. 이렇게하면 원본배열 arr을 사용하지 않아도 되므로 메모리를 더 아낄 수 있다. 역시 구현 방식의 차이이다.
void update(int ith, int diff) {
while (ith <= n) {
bit[ith] += diff;
ith += ith&-ith;
}
}
...
while (값 변경 쿼리마다) {
int idx = [변경할 인덱스];
long changeTo = [변경할 값];
int diff = changeTo - (getPrefixSum(idx) - getPrefixSum(idx-1))
update(idx, diff);
}
그럼 초기 데이터를 어떻게 삽입할지 알아보자. 애초에 초기값은 변화량(diff) 자체가 초기값 그 자체이다. 따라서 그냥 입력받으면서 위의 update 함수를 모든 인덱스 위치에 대해 호출해주면 된다. 단순히 아래와 같이 호출해주면 초기 데이터를 삽입해줄 수 있다.
for (int i = 1; i <= n; i++) {
update(i, arr[i]);
}
구현 2 : 구간합 획득(range query)
누적합 알고리즘으로 생각해보면, 결국 [1, B]의 합과 [1, A-1] 까지의 합을 안다면 [A, B]의 합은 '[1,B]합 - [1,A-1]합'으로 알 수 있음을 우린 이미 알고 있다. 그리고 펜윅 트리는 임의의 X 인덱스에 대해 모든 [1, X]의 값을 알 수 있으므로 구간합도 쉽게 알 수 있다. f(x)를 arr[1]부터 arr[x] 까지의 누적합이라 하면 다음과 같다.

만약 [1, 7]의 구간합을 알고 싶다면, 아래와 같이 3개의 값을 합치면 될 것이다. [1,7]합 = [7,7]합+[5,6]합+[1,4]합 = 16. 그림으로 따지면 저 녹색 바에서 좌측아래로만 계속 내려가주면 된다.

하나 더 해보자. [1,15]합은 다음과 같이 알 수 있다. [1,15]합 = [15,15]합+[13,14]합+[9,12]합+[1,8]합 = 29
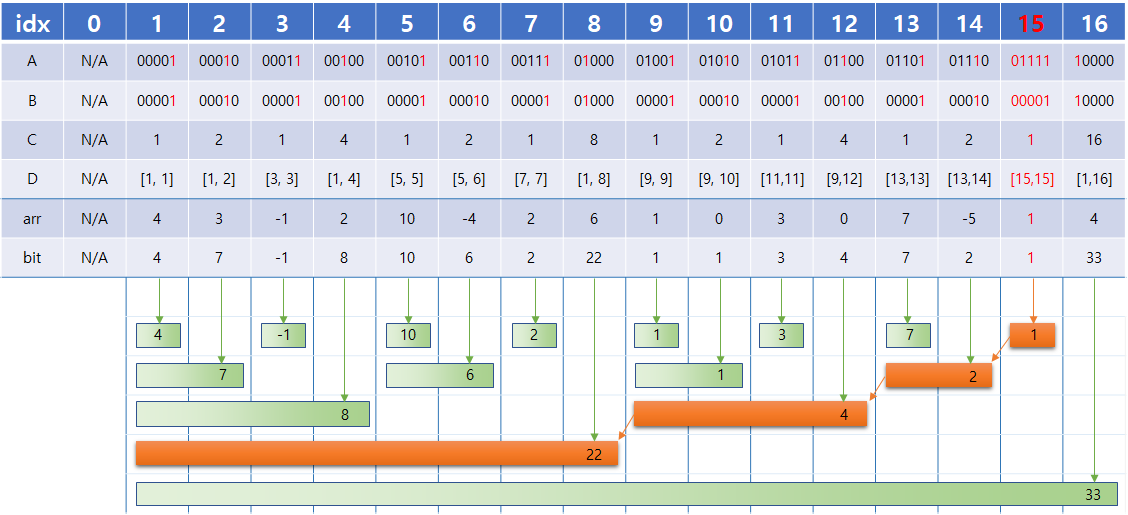
그럼 [8,15]합은 [1,15]합 - [1,7]합 이므로 29 - 16 = 13이다. 이처럼 2번의 누적합 쿼리 각 O(logN)으로 구간합을 계산할 수 있으므로 O(logN)에 구간합을 계산할 수 있다.
이것도 마찬가지로 2진수로 보면 규칙을 찾을 수 있다. [1,7]합은 인덱스 기준 7 -> 6 -> 4로 변화한다. 2진수로는 00111 -> 00110 -> 00100 으로 매번 가장 오른쪽 '1' 비트가 0으로 변경되면 되는걸 볼 수 있다. 이건 매번 맨 오른쪽 '1'에 -1을 해준 것과 같다(= 매번 맨 오른쪽 '1'만 남긴 것을 원래 값에서 빼줌). 이걸 남은 값이 0이 되기 전까지 계속 해주면 된다.
1. 00111 - 00001 = 00110
2. 00110 - 00010 = 00100
3. 00100 - 00100 = 00000 이므로 종료.
마찬가지로 [1,15]의 경우 인덱스 기준 15->14->12->8이고, 2진수로는 01111 -> 01110 -> 01100 -> 01000 이다.
1. 01111 - 00001 = 01110
2. 01110 - 00010 = 01100
3. 01100 - 00100 = 01000
4. 01000 - 01000 = 00000 이므로 종료.
어떻게 이런 자료구조를 생각했는지 다른 자료구조들도 그렇지만 펜윅트리가 개인적으로 정말 신기한 것 같다. 비트를 가지고 논다는게 이런 말인 것 같다.
구현은 논문의 경우엔 다음과 같다.

이걸 코드로 나타내면 다음과 같다.
int getPrefixSum(int ith) {
int answer = 0;
while (ith > 0) {
answer += bit[ith];
ith = ith&(ith-1);
}
return answer;
}
위의 코드로도 정상적으로 잘 작동하지만, 코드를 더 간결히 익히기 위해 값 변경 쿼리와 동일한 방식으로 구현해보면 다음과 같다. 위의 코드와 동일하게 동작한다.
int getPrefixSum(int ith) {
int answer = 0;
while (ith > 0) {
answer += bit[ith];
ith -= ith&-ith;
}
return answer;
}
마지막으로 위는 누적합을 계산하는 것이므로 [A, B]의 구간합은 다음과 같이 작성해주면 된다.
int query(int A, int B) {
return getPrefixSum(B) - getPrefixSum(A-1);
}
알고리즘 문제 예시
백준 2042 - 구간 합 구하기 문제를 예시로 보자.

중간중간 값 변경이 있는 구간합 쿼리 문제이다. 펜윅 트리로 당연히 구현할 수 있으며, 구현한 코드는 다음과 같다. 모두 설명한 내용이므로 코드를 보는데 큰 무리는 없을 것이라 생각된다.
Java
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private long[] bit, arr;
private int n;
private long query(int b, int c) {
return getPrefixSum(c) - getPrefixSum(b-1);
}
private long getPrefixSum(int ith) {
long answer = 0l;
while (ith > 0) {
answer += bit[ith];
ith -= ith&-ith;
}
return answer;
}
private void update(int ith, long val) {
long diff = val - arr[ith];
arr[ith] = val;
while (ith <= n) {
bit[ith] += diff;
ith += ith&-ith;
}
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
int mk = Integer.parseInt(st.nextToken()) + Integer.parseInt(st.nextToken());
arr = new long[n+1];
bit = new long[n+1];
for (int i = 1; i <= n; i++) {
update(i, Long.parseLong(br.readLine()));
}
StringBuilder sb = new StringBuilder();
while (mk-->0) {
st = new StringTokenizer(br.readLine());
switch (Integer.parseInt(st.nextToken())) {
case 1: update(Integer.parseInt(st.nextToken()), Long.parseLong(st.nextToken())); break;
case 2: sb.append(query(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()))).append('\n'); break;
}
}
System.out.print(sb);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}
C++
#include <iostream>
using namespace std;
#define ll long long
int n;
ll arr[1000001] = {0,};
ll bit[1000001] = {0,};
ll getPrefixSum(int ith) {
ll answer = 0l;
while (ith > 0) {
answer += bit[ith];
ith -= ith&-ith;
}
return answer;
}
ll query(int b, int c) {
return getPrefixSum(c) - getPrefixSum(b-1);
}
void update(int ith, long val) {
ll diff = val - arr[ith];
arr[ith] = val;
while (ith <= n) {
bit[ith] += diff;
ith += ith&-ith;
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int m, k;
cin >> n >> m >> k;
m += k;
for (int i = 1; i <= n; i++) {
ll cur;
cin >> cur;
update(i, cur);
}
while (m--) {
int a, b, c;
ll v;
cin >> a;
switch (a) {
case 1:
cin >> b >> v;
update(b, v);
break;
case 2:
cin >> b >> c;
cout << query(b, c) << '\n';
break;
}
}
}
응용 1 : 2차원 펜윅 트리
Two dimensional fenwick tree
누적합 알고리즘에서 2차원 배열에 대한 구간합을 구한 것과 동일하게 펜윅트리로도 (x1,y1) 부터 (x2,y2) 까지의 구간합을 구할 수 있다. 예를들어 아래 2차원 배열 데이터에서 (3,3)부터 (5,4)의 구간합은 21 이다.
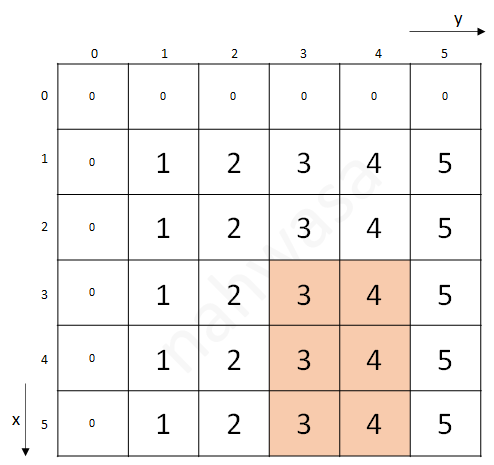
누적합 알고리즘과 마찬가지로 기본 펜윅트리를 칼럼 수 만큼 만들어서 계산할 수도 있다. 당연히 이 경우엔 시간복잡도에서 손해가 있기 때문에(RxC 크기라면 각 구간합 쿼리마다 O(RlogC)), 2차원으로 펜윅트리를 사용해 O(log(R+C))로 만들어보자.
개념은 2차원 누적합 알고리즘 설명할때와 완전히 동일하다. (1,1)부터 (x,y) 까지의 구간합을 알 수 있다면, (x1,y1)부터 (x2,y2) 까지의 구간합은 '(1,1)~(x2,y2)합 - (1,1)~(x1-1,y2)합 - (1,1)~(x2,y1-1)합 + (1,1)~(x1-1,y1-1)합'으로 구할 수 있다. 즉, 저 빨간부분의 합은 '전체 - 노란부분 - 녹색부분 + 노란부분과 녹색부분 겹치는부분 2번 빠졌으니 1번 더해줌' 이다.

펜윅트리로 이걸 구현한 예시를 보자.
- 값 변경 쿼리
누적합 알고리즘에서는 만약 값 변경이 필요할 경우, (x, y)가 변경되었다면 (x~N, y~N)에 해당하는 모든 값을 변경해줘야 한다. 하지만 펜윅트리는 2차원에서도 마찬가지로 logX * logY개만 변경해주면 된다. diff는 변화량이다. 구현은 기본 펜윅트리때와 동일한 방식을 2중으로 돌려주면 된다. 시간복잡도는 RxC 크기일 경우 O(logR x logC) 이다.
void update(int r, int c, int diff) {
while (r <= N) {
int cc = c;
while (cc <= N) {
bit[r][cc] += diff;
cc += cc&-cc;
}
r += r&-r;
}
}
- 누적합 획득 쿼리
(1,1)부터 (r,c) 까지의 누적합을 구하는 쿼리이다. 기본 펜윅 트리를 2중으로 사용 한 것 외에 차이가 없는걸 볼 수 있다. 마찬가지로 시간복잡도는 O(log(R+C)) 이다.
int getPrefixSum(int r, int c) {
int sum = 0;
while (r > 0) {
int cc = c;
while (cc > 0) {
sum += bit[r][cc];
cc -= cc&-cc;
}
r -= r&-r;
}
return sum;
}
- 구간합 획득 쿼리
누적합 알고리즘을 사용했을때와 동일한 방식으로 (x1,y1)부터 (x2,y2)의 구간합을 얻을 수 있다.
int query(int x1, int y1, int x2, int y2) {
return getPrefixSum(x2, y2) - getPrefixSum(x2, y1-1) - getPrefixSum(x1-1,y2) + getPrefixSum(x1-1, y1-1);
}
알고리즘 문제 예시
백준 11658 - 구간 합 구하기 3 문제를 예시로 보자.

중간중간 값 변경이 있는 2차원 구간합 쿼리 문제이다. 2차원 누적합 알고리즘으로 풀 경우 w=1 쿼리는 O(M)이지만, w=0 쿼리는 각각 O(N^2)이 되므로 총 O(M x N^2)이 되어 통과할 수 없다. 펜윅 트리로 구현 시 w=0쿼리와 w=1쿼리 모두 O(Mlog(2N)) 으로 통과 가능하다. 구현한 전체 코드는 다음과 같다.
Java
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
int N;
int[][] arr, bit;
private int getPrefixSum(int r, int c) {
int sum = 0;
while (r > 0) {
int cc = c;
while (cc > 0) {
sum += bit[r][cc];
cc -= cc&-cc;
}
r -= r&-r;
}
return sum;
}
private void update(int r, int c, int diff) {
while (r <= N) {
int cc = c;
while (cc <= N) {
bit[r][cc] += diff;
cc += cc&-cc;
}
r += r&-r;
}
}
private void initBit() {
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
update(i, j, arr[i][j]);
}
}
}
private int query(int x1, int y1, int x2, int y2) {
return getPrefixSum(x2, y2) - getPrefixSum(x2, y1-1) - getPrefixSum(x1-1,y2) + getPrefixSum(x1-1, y1-1);
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
arr = new int[N+1][N+1];
bit = new int[N+1][N+1];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= N; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
}
}
initBit();
StringBuilder sb = new StringBuilder();
while (m-->0) {
st = new StringTokenizer(br.readLine());
switch (Integer.parseInt(st.nextToken())) {
case 0:
int r = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
int val = Integer.parseInt(st.nextToken());
int diff = val - arr[r][c];
arr[r][c] = val;
update(r, c, diff);
break;
case 1:
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
sb.append(query(x1,y1,x2,y2)).append('\n');
}
}
System.out.print(sb);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}
C++
#include <iostream>
#include <string.h>
using namespace std;
int N;
int arr[1025][1025];
int bit[1025][1025];
int getPrefixSum(int r, int c) {
int sum = 0;
while (r > 0) {
int cc = c;
while (cc > 0) {
sum += bit[r][cc];
cc -= cc&-cc;
}
r -= r&-r;
}
return sum;
}
void update(int r, int c, int diff) {
while (r <= N) {
int cc = c;
while (cc <= N) {
bit[r][cc] += diff;
cc += cc&-cc;
}
r += r&-r;
}
}
int query(int x1, int y1, int x2, int y2) {
return getPrefixSum(x2, y2) - getPrefixSum(x2, y1-1) - getPrefixSum(x1-1,y2) + getPrefixSum(x1-1, y1-1);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int m;
cin >> N >> m;
memset(bit, 0, sizeof(bit));
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
cin >> arr[i][j];
update(i, j, arr[i][j]);
}
}
int op, a, b, c, d, diff;
while (m--) {
cin >> op;
if (op == 0) {
cin >> a >> b >> c;
diff = c - arr[a][b];
arr[a][b] = c;
update(a, b, diff);
} else {
cin >> a >> b >> c >> d;
cout << query(a,b,c,d) << '\n';
}
}
return 0;
}
응용 2 : 구간 업데이트, 단일 값 획득
range update + point query
원본 논문의 펜윅트리도 놀랍지만 그걸 응용해서 만든 이 알고리즘도 놀랍다.
기본 펜윅 트리는 point update + range query를 지원한다. 이걸로 '[A, B] 구간의 값을 6만큼 증가시키고, X번째 값의 현재 값을 획득한다.' 와 같은 질의에 대답해보자. 'X번째 값의 현재 값'같은 경우, [X, X]의 값 획득이라 볼 수 있으므로 기본 펜윅트리로도 문제없이 O(logN)에 가능하다. 하지만 [A, B] 구간의 값을 6만큼 증가시키려면 결국 O(NlogN)이 필요해지므로 시간이 많이 걸리게 된다. 이런류의 문제는 보통 세그먼트 트리로 lazy propagation 개념을 적용시켜 푸는 경우가 많다. 하지만 이하에 설명된 방식으로 펜윅트리를 응용하게되면 매우 간단하게 해결할 수 있다.
우선 펜윅 트리는 생각하지 말고, 그냥 원본 배열만 가지고 생각해보자.
arr이 원본 데이터가 있는 배열이다.
그리고 F라는 배열을 하나 정의해서 F[i] = arr[i] - arr[i-1] 이라고 해보자(인덱스가 1번부터 시작하는걸 기준으로 하므로 arr[0] = 0이다.).
1. [A, B] 구간의 값을 6만큼 증가 시킨다.
A=4, B=10 이라고 해보자. 그럼 원래 F[5] = arr[5] - arr[4] 일테고, arr[5]와 arr[4]는 둘 다 6만큼 증가되었으므로 6이 증가되면은, F[5]' = arr[5] + 6 - (arr[4] + 6) = arr[5] - arr[4] 이다. 즉 변화가 없다! 마찬가지로 F[6], F[7], F[8], F[9], F[10]은 변화가 없다. 변화가 생기는건 F[4]' = arr[4] + 6 - arr[3], F[11]' = arr[11] - (arr[10] + 6)의 두 곳 뿐이다.
정리하자면 arr의 [A, B] 구간의 값을 Y만큼 변화시키라는건 'F[A]를 Y만큼 증가시키고, F[B+1]을 Y만큼 감소시켜라'가 된다. 즉 range update가 point update로 변경된 셈이다. (B+1이 배열 길이를 넘어설 경우는 F[B+1]은 없으므로 무시하면 된다.)
2. X번째 값의 현재 값 획득
X가 5라고 해보자. arr[5]의 값을 F를 사용해 어떻게 알 수 있을까? F[1]부터 F[5]까지를 모두 더해주면 된다.
F[1] + F[2] + F[3] + F[4] + F[5] = arr[1] - 0 + arr[2] - arr[1] + arr[3] - arr[2] + arr[4] - arr[3] + arr[5] - arr[4] = arr[5]
정리하자면 arr의 X번째 값을 획득하라는건 'F[1] + F[2] + ... + F[X] 의 값을 획득하라'가 된다. 즉 point update가 range query로 변경된 셈이다.(arr[X] = F[1] + ... + F[X])
그럼 펜윅트리로 위를 구현하려면, 배열 F를 기준으로 펜윅트리를 구현해주면 된다는걸 알 수 있다. 즉 정확힌 펜윅트리를 응용했다기 보다는, range update + point query를 point update + range query로 변경하는 일종의 배열 테크닉을 사용한거고, 어쨌든 point update + range query로 변경된 배열이라면 펜윅트리를 적용할 수 있으니 펜윅트리를 사용할 수 있게 된 것이다.
응용 2를 구현해보면 다음과 같다. update와 query는 기존 펜윅의 구현과 안전히 동일하며(단, query가 기존엔 누적합을 리턴했다면, arr[i]를 리턴한다.), update 시 rangeUpdate()를 호출해 위에서 말한대로 시작점과 끝점+1에 대해서만 update를 해주면 된다.
void update(int i, int diff) {
while (i <= n) {
bit[i] += diff;
i += i&-i;
}
}
int query(int i) {
int sum = 0;
while (i > 0) {
sum += bit[i];
i -= i&-i;
}
return sum;
}
void rangeUpdate(int i, int j, int diff) {
update(i, diff);
update(j+1, -diff);
}
이 때 주의점은, 기본 펜윅 트리는 '값을 X만큼 증가시켜라' 라거나 '값을 X로 변경해라' 둘 다 대응이 가능하지만, 응용 2(응용 3도 마찬가지)의 경우엔 전자에 대해서만 처리할 수 있다. 후자의 경우에는 arr의 각 값마다 변화량이 다를 것이므로 응용의 방법을 적용시킬 수 없다. 예를들어 [1,2,3,4] 라는 배열에 있을 때 2번째부터 4번째 값의 값을 5로 변경하라는 말은 2번째값은 +3, 3번째값은 +2, 4번째값은 +1이 되므로 F 배열을 적용시킬 수 없다. 이건 근데 세그먼트 트리에 lazy propagation을 적용해도 마찬가지로 대응할 수 없어서 애초에 다른 방법으로 풀어야할 것 같다.
단, 값의 변화가 등차수열 형태라면 적용이 가능하다. 이 글의 풀이를 참고하자.
알고리즘 문제 예시
백준 16975 - 수열과 쿼리 21 문제를 예시로 보자.
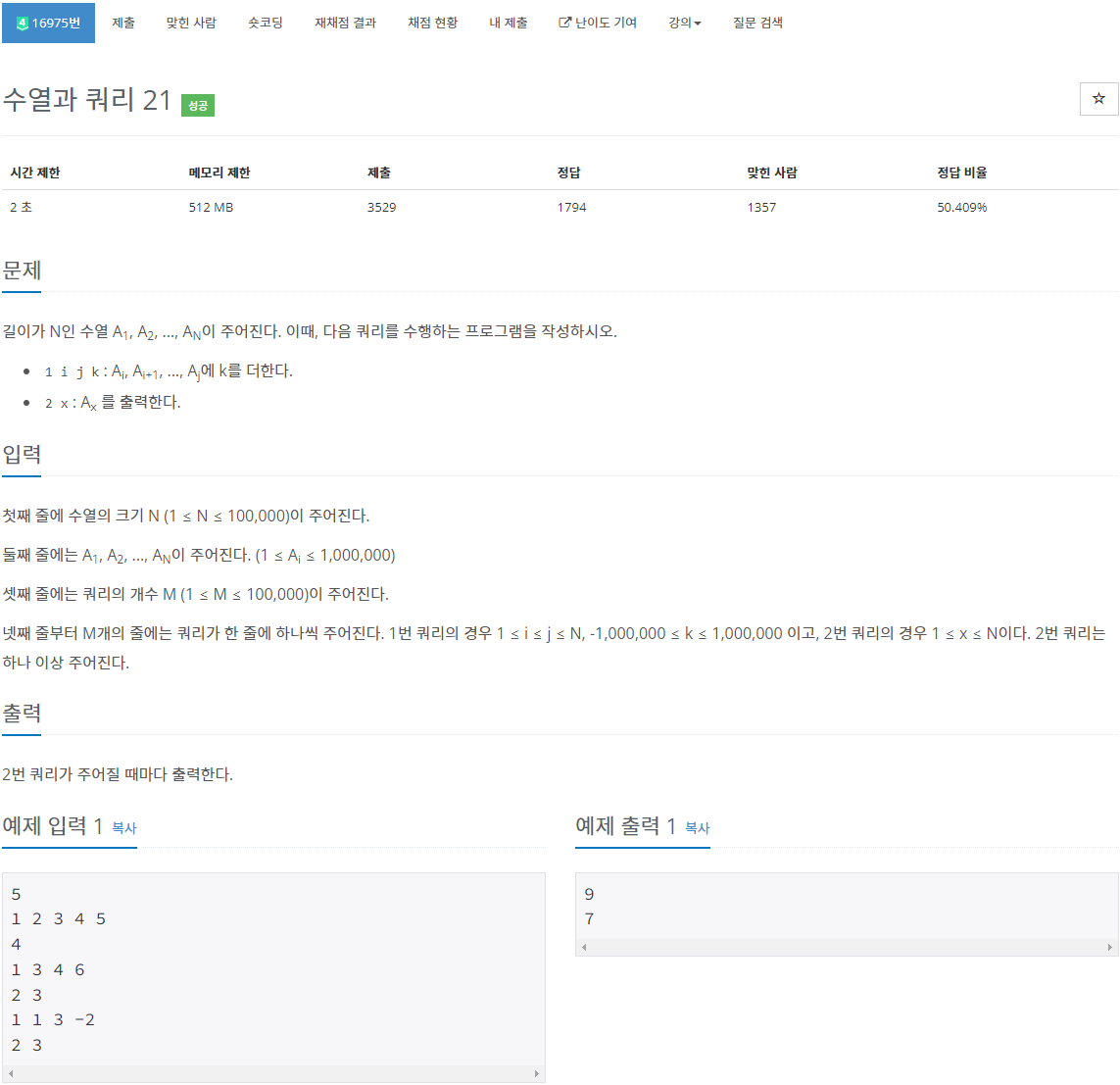
응용 2에서 설명한대로 range update와 point query에 해당하는 기본형태의 문제이다. 구현한 코드는 아래와 같다.
Java
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
int n;
long[] bit;
private void update(int i, long diff) {
while (i <= n) {
bit[i] += diff;
i += i&-i;
}
}
private long query(int i) {
long sum = 0;
while (i > 0) {
sum += bit[i];
i -= i&-i;
}
return sum;
}
private void rangeUpdate(int i, int j, long diff) {
update(i, diff);
update(j+1, -diff);
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
bit = new long[n+1];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) {
rangeUpdate(i, i, Integer.parseInt(st.nextToken()));
}
int m = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
while (m-->0) {
st = new StringTokenizer(br.readLine());
switch (Integer.parseInt(st.nextToken())) {
case 1: rangeUpdate(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken())); break;
case 2: sb.append(query(Integer.parseInt(st.nextToken()))).append('\n'); break;
}
}
System.out.print(sb);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}
C++
#include <iostream>
using namespace std;
#define ll long long
int n;
ll bit[100001] = {0,};
void update(int i, ll diff) {
while (i <= n) {
bit[i] += diff;
i += i&-i;
}
}
ll query(int i) {
ll sum = 0;
while (i > 0) {
sum += bit[i];
i -= i&-i;
}
return sum;
}
void rangeUpdate(int i, int j, ll diff) {
update(i, diff);
update(j+1, -diff);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int m;
cin >> n;
for (int i = 1; i <= n; i++) {
ll cur;
cin >> cur;
rangeUpdate(i, i, cur);
}
cin >> m;
while (m--) {
int op, a, b, c;
cin >> op;
switch (op) {
case 1:
cin >> a >> b >> c;
rangeUpdate(a, b, c);
break;
case 2:
cin >> a;
cout << query(a) << '\n';
break;
}
}
}
응용 3 : 구간 업데이트, 구간 값 획득
range update + range query
개인적으로 이해하는게 많이 어려웠다. 생각해낸 사람이 정말 대단하다.. 여러 글들 찾아봐도 다들 상세하게 안적어주고 대강 실력 있으니 알아서 보겠지 싶은건지 대강 퉁치고 넘어가는 바람에 내 경우엔 수학이 약해서 이해하는데 몇일 걸렸다 ㅠ. 이번엔 [A, B]를 Y만큼 변경하고, [A, B]의 구간합을 획득하는 range update + range query에 대해 알아보자. 응용2가 사용되므로, 응용2를 먼저 이해한 후 봐야 이해가 가능하다.
arr의 누적합인 P를 생각해보자(P[i] = arr[1]+arr[2]+...+arr[i]). 이 때 설명의 편의를 위해 arr에는 현재 초기값이 0이라고 가정하자. 즉, P의 모든 값도 현재 0인 상태이다. (그럼 초기값 없는 문제만 풀 수 있겠네? 라고 할 수 있으나, 초기값도 [X, X]에 대한 range update라고 생각하고 update 해주면 된다.)
1. 이 때, [A, B]의 값이 Y 만큼 변경 된다고 해보자.
임의의 인덱스 X에 대해 P[X]의 변경값은 다음과 같다. 예를들어 A<=X<=B 인 경우 [A,X]구간에 대해 Y만큼씩 증가되므로 [A,X]는 (X-A+1)개의 구간이고, 각각 Y만큼 증가되니 P[X]는 Y(X-A+1)만큼 증가 된다.

2. 이 때, arr[X] = P[X] - P[X-1] 이므로 다음과 같다.
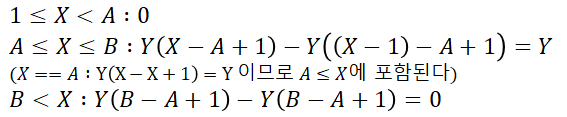
3. 그렇다면 X*arr[X]은 A<=X<=B 일 때만 XY이고, 나머진 0이다. 그럼 '1'의 식을 X*arr[X] - Z 의 꼴로 나타내보자. 즉, P[X]를 '1'과 '2'를 합쳐서 X*arr[X]-Z 꼴이 되도록 한 것이다.

위와 같이 진행할 시, P[X]를 알기 위해 필요한 것은 arr[X]값과 Z값이 된다. 그럼 이걸 알기 위해 '응용 2'의 펜윅 트리 2개를 사용해서 'BIT1'에 arr[X], 'BIT2'에 Z를 각각 저장하자. 이 때 'BIT1'은 기존 '응용 2' 처럼 arr에 대해 F1[i] = arr[i] - arr[i-1] 로 정의한 형태의 F1을 가지고 펜윅트리를 돌린 것이고, 'BIT2'는 arr의 누적합인 P에 대해 F2[i] = P[i] - P[i-1] 로 정의한걸 사용한다.(아무도 이걸 안써줬다.. 이해하기 빡쌨다 ㅠ).
그래서 'BIT1'에 대한 구현은 arr[X]에 대한 point query였던 '응용 2'와 완전히 동일하다. 'BIT2'의 경우엔 arr[x]의 변화에 따른 P[x]의 변화를 저장한 것이고, 이건 '3'에서 봤듯이 구간에 따라 Z값의 변화량이 다르다. 하지만 개념은 '응용 2'와 동일하게 [A,B] 구간 변경이라면 BIT2[A]에는 변화량+, BIT2[B+1]에는 변화량- 해주는 것이다.
1<=X<A 에 대해 1번 인덱스에 +0, A번 인덱스에 -0
A<=X<=B에 대해 A번 인덱스에 +Y(A-1), B+1 인덱스에 -Y(A-1)
B<X에 대해 B+1인덱스에 -YB+Y(A-1)
을 해줘야 한다. 따라서 B+1 인덱스에 대해서는 -YB+Y(A-1)-Y(A-1)이 되어 -YB만 저장해주면 된다.
이렇게 응용3을 구현한 코드는 아래와 같다.
void update(int bitType, int idx, int diff) {
int* bit = bitType==1 ? bit1 : bit2; // Java는 int[]
while (idx <= n) {
bit[idx] += diff;
idx += idx&-idx;
}
}
void rangeUpdate(int a, int b, int diff) {
update(1, a, diff);
update(1, b+1, -diff);
update(2, a, diff * (a-1));
update(2, b+1, -diff * b);
}
int getBitValue(int bitType, int idx) {
int* bit = bitType==1 ? bit1 : bit2; // Java는 int[]
int answer = 0;
while (idx > 0) {
answer += bit[idx];
idx -= idx&-idx;
}
return answer;
}
int prefixSum(int idx) {
return getBitValue(1, idx) * idx - getBitValue(2, idx);
}
int query(int a, int b) {
return prefixSum(b) - prefixSum(a-1);
}
rangeUpdate()를 통해 위에서 말한대로 BIT1에 arr[X]를 저장하고, BIT2에 Z를 저장한다. 그리고 위에서 본 '3'ㅇ 식은 prefixSum()에서 볼 수 있고, 이걸 통해 역시 말한대로 P[X]를 구하고 있다. 최종적으로 query() 함수에서 [A, B]의 구간합은 P[B]-P[A-1]이므로 range update + range query가 가능하다.
알고리즘 문제 예시
백준 10999 - 구간 합 구하기 2 문제를 예시로 보자.

응용 3에서 설명한 것과 같이 range update + range query로 된 기본형태의 문제이다. 구현한 코드는 아래와 같다.
Java
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
long[] bit1, bit2;
int n;
private void update(int bitType, int idx, long diff) {
long[] bit = bitType==1 ? bit1 : bit2;
while (idx <= n) {
bit[idx] += diff;
idx += idx&-idx;
}
}
private void rangeUpdate(int a, int b, long diff) {
update(1, a, diff);
update(1, b+1, -diff);
update(2, a, diff * (a-1));
update(2, b+1, -diff * b);
}
private long getBitValue(int bitType, int idx) {
long[] bit = bitType==1 ? bit1 : bit2;
long answer = 0;
while (idx > 0) {
answer += bit[idx];
idx -= idx&-idx;
}
return answer;
}
private long prefixSum(int idx) {
return getBitValue(1, idx) * idx - getBitValue(2, idx);
}
private long query(int a, int b) {
return prefixSum(b) - prefixSum(a-1);
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
bit1 = new long[n+1];
bit2 = new long[n+1];
int mk = Integer.parseInt(st.nextToken()) + Integer.parseInt(st.nextToken());
for (int i = 1; i <= n; i++) {
rangeUpdate(i, i, Long.parseLong(br.readLine()));
}
StringBuilder sb = new StringBuilder();
while (mk-->0) {
st = new StringTokenizer(br.readLine());
switch (Integer.parseInt(st.nextToken())) {
case 1:
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
long diff = Long.parseLong(st.nextToken());
rangeUpdate(a, b, diff);
break;
case 2:
int i = Integer.parseInt(st.nextToken());
int j = Integer.parseInt(st.nextToken());
sb.append(query(i, j)).append('\n');
break;
}
}
System.out.print(sb);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}
C++
#include <iostream>
using namespace std;
#define ll long long
int n;
ll bit1[1000001] = {0,};
ll bit2[1000001] = {0,};
void update(int bitType, int idx, long diff) {
ll* bit = bitType==1 ? bit1 : bit2;
while (idx <= n) {
bit[idx] += diff;
idx += idx&-idx;
}
}
void rangeUpdate(int a, int b, long diff) {
update(1, a, diff);
update(1, b+1, -diff);
update(2, a, diff * (a-1));
update(2, b+1, -diff * b);
}
ll getBitValue(int bitType, int idx) {
ll* bit = bitType==1 ? bit1 : bit2;
long answer = 0;
while (idx > 0) {
answer += bit[idx];
idx -= idx&-idx;
}
return answer;
}
ll prefixSum(int idx) {
return getBitValue(1, idx) * idx - getBitValue(2, idx);
}
ll query(int a, int b) {
return prefixSum(b) - prefixSum(a-1);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
int m, k;
cin >> n >> m >> k;
m += k;
for (int i = 1; i <= n; i++) {
ll cur;
cin >> cur;
rangeUpdate(i, i, cur);
}
while (m--) {
int op, a, b;
ll v;
cin >> op;
switch (op) {
case 1:
cin >> a >> b >> v;
rangeUpdate(a, b, v);
break;
case 2:
cin >> a >> b;
cout << query(a, b) << '\n';
break;
}
}
}
주의점 및 관련 문제들
주의점
펜윅 트리는 원본 데이터의 수 N이 2의 제곱수가 아니라도 추가로 2의 제곱수에 맞춰서 공간을 만들지 않아도 전혀 상관없다. 그냥 위의 구현 그대로 사용 가능하다. 예를들어 N이 12인 경우 다음과 같이 그려질 것이다. 전체를 한번에 표현하는 누적합(기존 16번 idx 처럼)은 없지만, 전체의 합도 [9,12]합 + [1,8]합으로 문제없이 구할 수 있음을 볼 수 있다.

누적합 알고리즘과 마찬가지로 데이터의 합 혹은 계산 중간에 정수 표현형의 최대 표현 범위를 넘으면 안된다. 예를들어 백준 2042번 구간 합 구하기 문제의 경우, '정답은 -2^63보다 크거나 같고, 2^63-1보다 작거나 같은 정수이다.' 라는 조건을 통해 모든 데이터의 합이 long 데이터 타입의 범위를 넘어서지 않음을 보장하고 있다. 만약 long의 범위를 넘어가는 수에 대해 펜윅 트리를 사용해야 할 경우 각 언어의 큰 수 자료형(예를들어 자바는 BigInteger)을 쓰거나, 정신건강상 파이썬을 쓰자.
관련 문제
백준 2042 : 구간 합 구하기
백준 7578 : 공장
백준 11658 : 구간 합 구하기 3
백준 16975 : 수열과 쿼리 21
백준 2820 : 자동차 공장
백준 10999 : 구간 합 구하기 2
백준 1517 : 버블 소트
펜윅 트리 기본 형태의 문제이다 (분할 정복으로도 풀 수 있다.)
다만 아이디어가 좀 필요하고(Inversion Counting), 좌표 압축 등도 필요해서 재밌다.
백준 2835 : 인기도 조사
응용3을 사용해 바로 풀 수 있다.
다만, 그것 때문에 관련 문제에 넣어둔건 아니고 응용2에 나온 설명을 참고해서 펜윅트리를 아예 쓰지 말고
풀어보자! 응용2에 나온 설명을 응용해서(?) 누적합 알고리즘으로 풀 수 있는 문제이다.
백준 17353 : 하늘에서 떨어지는 1, 2, ..., R-L+1개의 별
응용2 또는 응용3으로 풀 수 있다.
하지만 변화량이 동일하지 않고, [L,R]에 대해 차례대로 1,2,...,R-L+1 만큼 변화한다. 즉 등차수열 형태로 변화하는 수치일 경우에 해당한다. 한번 어떻게 할지 생각해보자.
References
1. Fenwick, Peter M. 1994. A new data structure for cumulative frequency tables. Software: Practice and Experience, 24(3), 327–336.
2. https://cp-algorithms.com/data_structures/fenwick.html
Fenwick Tree - Algorithms for Competitive Programming
Fenwick Tree Let, \(f\) be some group operation (binary associative function over a set with identity element and inverse elements) and \(A\) be an array of integers of length \(N\). Fenwick tree is a data structure which: calculates the value of function
cp-algorithms.com
3. https://www.topcoder.com/thrive/articles/Binary Indexed Trees
Binary Indexed Trees
Discuss this article in the forums Introduction Notation Basic idea Isolating the last bit Read cumulative fre
www.topcoder.com
4. https://www.acmicpc.net/blog/view/21
펜윅 트리 (바이너리 인덱스 트리)
블로그: 세그먼트 트리 (Segment Tree) 에서 풀어본 문제를 Fenwick Tree를 이용해서 풀어보겠습니다. Fenwick Tree는 Binary Indexed Tree라고도 하며, 줄여서 BIT라고 합니다. Fenwick Tree를 구현하려면, 어떤 수 X
www.acmicpc.net
5. https://www.geeksforgeeks.org/two-dimensional-binary-indexed-tree-or-fenwick-tree/
Two Dimensional Binary Indexed Tree or Fenwick Tree - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
6. https://www.acmicpc.net/blog/view/88
펜윅 트리 200% 활용하기
흔히 lazy propagation을 사용하여 푸는 것으로 알려진 이 두 문제는 사실 펜윅 트리만으로 풀 수 있습니다. 구간 덧셈, 포인트 쿼리 다음 연산을 효율적으로 수행하는 자료구조를 만들어 봅시다. 이
www.acmicpc.net
7. https://petr-mitrichev.blogspot.com/2013/05/fenwick-tree-range-updates.html
Fenwick tree range updates
A Fenwick tree is a wonderful data structure that supports two operations on an array: increment a given value by a given amount, and find...
petr-mitrichev.blogspot.com
8. https://www.geeksforgeeks.org/binary-indexed-tree-range-update-range-queries/
Binary Indexed Tree : Range Update and Range Queries - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
9. https://kartikkukreja.wordpress.com/2013/12/02/range-updates-with-bit-fenwick-tree/
Range updates with BIT / Fenwick Tree
I described implementation of BIT/Fenwick tree in an earlier post as a way of maintaining cumulative frequency table, which allows operations like updating any single element and querying sum of el…
kartikkukreja.wordpress.com
10. https://www.crocus.co.kr/666
펜윅 트리(Fenwick Tree, Binary Indexed Tree, BIT)
펜윅 트리(Fenwick Tree, Binary Indexed Tree, BIT)란? 이전 게시물에서는 세그먼트 트리에 대해 게시물을 올렸다. (세그먼트 트리 :: http://www.crocus.co.kr/648) 이 펜윅 트리를 이해하기 위해서는 세그먼트..
www.crocus.co.kr
11. https://codeforces.com/blog/entry/52094
Easy implementation of Compressed 2D Binary Indexed Tree for grid of binary numbers[Tutorial] - Codeforces
codeforces.com
'CS > Data structures' 카테고리의 다른 글
| [자료구조] C언어 - 이진 탐색 트리(BST , binary search tree) 구현 - 객체지향 (0) | 2022.04.09 |
|---|---|
| [자료구조] C언어 - 우선순위 큐(priority queue) 구현 - 객체지향 (0) | 2022.04.09 |
| [자료구조] C언어 - 큐(queue) 구현 - 객체지향 (0) | 2022.04.09 |
| [자료구조] C언어 - 스택(stack) 구현 - 객체지향 (0) | 2022.04.09 |
| [자료구조] C언어 - 다항식(polynomial) 구현 - 객체지향 (0) | 2022.04.09 |





댓글