문제 : boj14428
가장 간단하게 생각할 수 있는 방법인 brute force부터 확인해보자. 10만개의 N개가 주어지고, 모든 쿼리가 '2 1 100000' 이런식이라면 O(NM)이 필요할 것이다. 따라서 시간내에 통과할 수 없다. 사실 이런식으로 중간중간 값이 변경되고, 범위에 대한 쿼리를 출력하는 유형은 대표적으로 세그먼트 트리(segment tree)를 사용하는 문제이다. 내 경우엔 조금 더 비효율적이지만, 훨씬 간단하고 구현을 이해하기 편하다고 생각되는 sqrt decompositon 방식을 사용해서 풀어봤다.
1. Sqrt decomposition 초기화 (코드의 init 함수)
이론적으론 세그먼트 트리에 비해 이해하기가 엄청 간단하다. 특정 수열이 N개의 수를 가진다면 N의 제곱근만큼 잘라서 구역을 만든다(그럼 전체 구역은 sqrt(N)개이고, 각 구역에 포함되는 수열 또한 sqrt(N)개가 된다.). 그리고 해결하려는 쿼리에 맞게 해당 구역에 필요한 데이터를 별도로 유지한다. 예를들어서 구간합 문제라면 해당 구역에 있는 sqrt(N)개의 합을 저장하는 1차원 배열이면 될 것이다. 이 문제의 경우 해당 구간 중 가장 작은 값의 인덱스를 알아야 하므로 2차원 배열로 최소값과, 해당 최소값의 인덱스를 기억하도록 했다.

2. update 쿼리 구현 (코드의 update 함수)
'1 i v' 형태의 update 쿼리를 구현해보자. 이 때, sqrt(N)개씩 구역을 나눴으므로 구역 번호는 i/sqrt(N) 으로 알 수 있다. 그럼 다음의 경우들이 있을 것이다.
A. v가 해당 구역에 저장해둔 최소값보다 작은 경우
-> 뭐 생각할 것 없이 해당 구역의 최소값 idx와 최소값만 변경하면 된다. O(1)
B. v가 해당 구역 최소값과 동일하지만 인덱스가 더 작은 경우
-> 역시 해당 구역의 최소값 idx만 변경하면 된다. O(1)
C. i가 해당 구역 최소값 idx와 동일하면서 최소값보다 큰 경우. 즉 기존 최소값이었던 인덱스가 변경된 경우이다.
-> 이 경우엔 해당 구역 전체를 재확인 해야 한다. O(sqrt(N))
참고로 이 문제의 경우 'C'처럼 해당 구역 전체를 매번 재확인해도 통과 가능하다. A, B는 약간 더 효율성을 좋게 하기 위해 추가한 조건들이다.
3. 쿼리 결과 출력 (코드의 query 함수)
'2 i j' 형태의 쿼리를 구현해보자. '1'에서 봤던 이미지에서 전체에 대한 쿼리가 들어왔다고 해보자. 즉, '2 1 9'와 같은 쿼리이다. 이 경우 모든 구간이 나눠둔 구역내에 포함되므로, 구역에 대해 저장해둔 최소값들만 확인하면 쿼리를 해결할 수 있다. 구역의 개수가 sqrt(N)개 이므로 O(sqrt(N))이 걸린다.
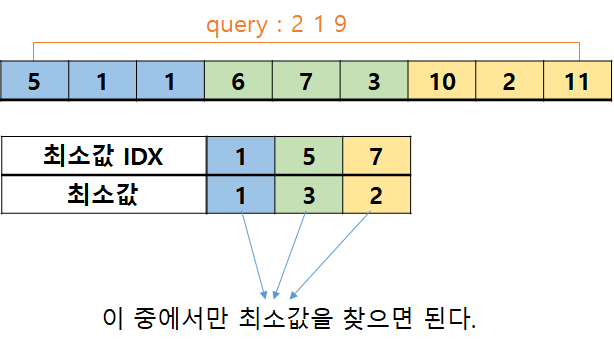
그럼 이번엔 구역이 중간에 걸친 경우를 확인해보자. '2 3 8'과 같은 경우이다. 이 경우에 구역 전체가 포함되는 4~6 부분은 저장된 값을 사용하면 되고, 나머지 구역에 걸친 부분은 실제 값을 확인하면 된다. 이 경우도 마찬가지로 해당 구역내에 포함되는 수의 개수가 sqrt(N)개 이고, 구역의 개수도 sqrt(N)개 이므로 O(sqrt(N)+sqrt(N)+sqrt(N)) = O(sqrt(N))이 된다.

결론적으로 update 및 쿼리 결과 연산 모두 O(sqrt(N)) 내에 처리가 가능하게 되므로 O(Msqrt(N))의 시간복잡도가 나오므로 세그먼트 트리의 O(MlogN) 보다는 다소 비효율적이지만 이 문제에는 문제없이 적용 가능하다. 사실 세그에 비해 좀 더 이해하고 구현하기 편하다는 점이 장점이지, 그렇다고 구현이 엄청 쉬운것도 아니다 ㅋㅋ 코드를 참고해보자. sqrt decomposition에 대해 더 자세히 알려면 여기를 참고하면 된다. (mo's algorithm 나오기 이전 부분까지만 보면 된다.)
log 기반 복잡도와 sqrt 기반 복잡도를 비교해보자. 확실히 log쪽이 더 효율적이다.

뭐 이 문제의 제한인 10만쯤 가게되면 어찌됬든 y=x 에 비해 둘다 충분히 효율적이다.

코드 : github
import java.io.DataInputStream;
import java.io.IOException;
import java.util.Arrays;
public class Main extends FastInput {
int n, sqrtN;
int[] arr;
int[][] bucket; //[][0]: min idx, [][1]: min value
private void init() {
sqrtN = (int) Math.sqrt(n);
bucket = new int[n/sqrtN+(n%sqrtN==0?0:1)][2];
for (int[] tmp : bucket) Arrays.fill(tmp, Integer.MAX_VALUE);
for (int i = 0; i < n; i++) {
int idx = i/sqrtN;
if (arr[i]<bucket[idx][1]) {
bucket[idx][1] = arr[i];
bucket[idx][0] = i;
}
}
}
private void update(int i, int v) {
int idx = i/sqrtN;
arr[i] = v;
if (v==bucket[idx][1] && i<bucket[idx][0]) { // same value, but small idx
bucket[idx][0] = i;
} else if (v<bucket[idx][1]) { // small value
bucket[idx][0] = i;
bucket[idx][1] = v;
} else if (bucket[idx][0]==i && v>bucket[idx][1]) { // same idx and bigger value
// reset bucket
bucket[idx][1] = Integer.MAX_VALUE;
for (int j = idx*sqrtN; j < (idx+1)*sqrtN && j < n; j++) {
if (arr[j]<bucket[idx][1]) {
bucket[idx][1] = arr[j];
bucket[idx][0] = j;
}
}
}
}
private int query(int a, int b) {
int minIdx = Integer.MAX_VALUE;
int minVal = Integer.MAX_VALUE;
while (a%sqrtN!=0 && a<=b) {
if (arr[a]<minVal) {
minIdx = a;
minVal = arr[a];
}
a++;
}
while ((b+1)%sqrtN!=0 && a<=b) {
if (arr[b]<minVal) {
minIdx = b;
minVal = arr[b];
} else if (arr[b]==minVal && b<minIdx) {
minIdx = b;
}
b--;
}
for (int i = a/sqrtN; i < (b+1)/sqrtN; i++) {
if (bucket[i][1]<minVal) {
minIdx = bucket[i][0];
minVal = bucket[i][1];
} else if (bucket[i][1]==minVal && bucket[i][0]<minIdx) {
minIdx = bucket[i][0];
}
}
return minIdx;
}
private void solution() throws Exception {
n = nextInt();
arr = new int[n];
for (int i = 0; i < n; i++)
arr[i] = nextInt();
init();
int m = nextInt();
StringBuilder sb = new StringBuilder();
while (m-->0) {
int q = nextInt();
int a = nextInt();
int b = nextInt();
switch (q) {
case 1: update(a-1, b); break;
case 2: sb.append(query(a-1, b-1)+1).append('\n'); break;
}
}
System.out.print(sb);
}
public static void main(String[] args) throws Exception {
initFI();
new Main().solution();
}
}
class FastInput {
private static final int DEFAULT_BUFFER_SIZE = 1 << 16;
private static DataInputStream inputStream;
private static byte[] buffer;
private static int curIdx, maxIdx;
protected static void initFI() {
inputStream = new DataInputStream(System.in);
buffer = new byte[DEFAULT_BUFFER_SIZE];
curIdx = maxIdx = 0;
}
protected static int nextInt() throws IOException {
int ret = 0;
byte c = read();
while (c <= ' ') c = read();
do {
ret = ret * 10 + c - '0';
} while ((c = read()) >= '0' && c <= '9');
return ret;
}
private static byte read() throws IOException {
if (curIdx == maxIdx) {
maxIdx = inputStream.read(buffer, curIdx = 0, DEFAULT_BUFFER_SIZE);
if (maxIdx == -1) buffer[0] = -1;
}
return buffer[curIdx++];
}
}'PS > BOJ' 카테고리의 다른 글
| 백준 1339 자바 - 단어 수학 (BOJ 1339 JAVA) (0) | 2022.02.15 |
|---|---|
| 백준 11292 자바 - 키 큰 사람 (BOJ 11292 JAVA) (0) | 2022.02.14 |
| 백준 6219 자바 - 소수의 자격 (BOJ 6219 JAVA) (0) | 2022.02.12 |
| 백준 2358 자바 - 평행선 (BOJ 2358 JAVA) (0) | 2022.02.11 |
| 백준 11653 파이썬 - 소인수분해 (BOJ 11653 Python) (0) | 2022.02.10 |





댓글