문제 : boj10986

필요 알고리즘 개념
- 수학, 누적 합
- 수학적 사고를 통해 어떻게 구할 수 있을지 생각할 수 있어야 한다. 내 경우엔 해당 풀이를 구현하기 위해 누적합 알고리즘을 사용했다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
필요 개념
이하 풀이에는 누적합 알고리즘이 필요하므로 모른다면 이 글을 참고하자. 2차원 누적합까진 안봐도 된다.
또 이 문제를 풀기 위해 알고있어야 하는 법칙이 있다. 나머지를 가지고 노는 여러 문제에서 제일 중요한 개념이라 이참에 익혀두자. 어떠한 정수 A와 B에 대해 A+B를 M으로 나눈 나머지는 'A를 M으로 나눈 나머지 + B를 M으로 나눈 나머지'를 다시 M으로 나눈 나머지와 동일하다는 얘기이다.
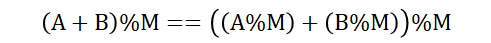
음수에 대해서도 적용이 가능하긴 한데, 괄호 안쪽이 음수가 되지 않도록 주의해야 한다. (음수에 대한 나머지 연산이 언어마다 결과가 다르므로 구현이 복잡해진다)
(A-B)%M == ((A%M) - (B%M))%M 이긴한데, 음수에 대한 나머지 연산에 대해 언어마다 결과가 다른 문제가 있으므로 간단히 위의 덧셈에 대한 분배를 추가로 적용해서 음수가 되지 않도록 해주면 된다. (A-B)%M == ((A%M) - (B%M) + M)%M 으로 고쳐서 사용하면 된다. M%M은 어차피 0이므로 '+M'을 추가해도 결과에 영향을 끼치지 않는다.(이하 풀이에서는 이 '+M' 부분에 대해 추가로 언급하지 않을건데, 어차피 나누어 떨어지는 경우만 볼 것이기 때문이므로 음수가 발생할 수 없기 때문이다.)
풀이
문제에 제시된 '연속된 부분 구간의 합이 M으로 나누어 떨어지는' 이라는 부분이 어떤 의미를 가질지 생각해보자. 어떠한 구간 [a, b]에 대해 '[a, b] 구간합 == [1, b] 구간합 - [1, a-1] 구간합' 임은 당연하다. arr[x]를 '[1, x]의 구간합' 이라고 정의하자. 그렇다면 '연속된 부분 구간의 합이 M으로 나누어 떨어진다'라는 말을 수식으로 적어보면 '(arr[b] - arr[a-1])%M == 0' 이 된다. (문제에서는 i와 j이지만 글로 적을 때 알아보기 힘드므로 a,b로 변경했다.)
그렇다면 '필요 개념'에 따라 아래처럼 적용해볼 수 있다.

이 때, 문제 조건에 따라 좌변이 0이 되어야 하므로, 우변 또한 0이 되어야 하고, '(arr[b]%M) - (arr[a-1]%M) == 0' 이라고 할 수 있다. 따라서 구간 [a, b]에 대해 'arr[b]%M == arr[a-1]%M' 이라면 [a, b]의 구간합은 M으로 나누어 떨어진다.
그렇다면, 만약 x = 1부터 N 까지 순서대로 입력받으면서 누적합을 구하고, 모든 x 위치에서의 [1, x]의 구간합을 M으로 나눈 나머지를 알고 있다면 어떨까? 현재 x값에 대해 누적합을 M으로 나눈 나머지와 동일한 값이 이전에 나왔던 경우의 수를 세면 이 문제의 답을 구할 수 있을 것이다.
예제 입력 1을 생각해보자.
5 3
1 2 3 1 2표로 필요한 데이터들을 적어보면 아래와 같다.

위 표를 통해 모든 x값에 대해 [1, x]의 구간합을 M으로 나눈 나머지를 알게되었다. 이걸 가지고 답을 구할 수 있다.
1. x=1
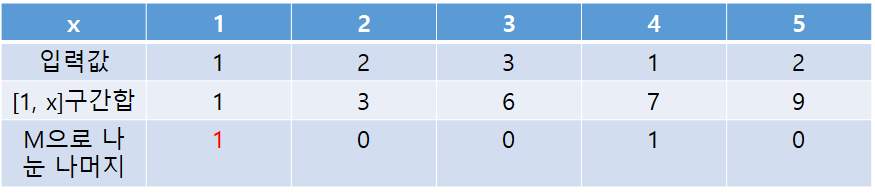
이 때는 문제의 조건을 만족하는 부분이 없다. answer = 0
2. x=2
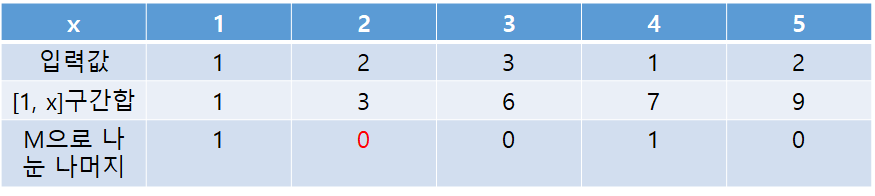
이 때에도 문제의 조건을 만족하는 부분은 없다. 다만, M으로 나눈 나머지가 0일때는 중간의 구간이 아니라 그냥 처음부터 x까지의 합이 M으로 나누어 떨어지는 경우이다. 따라서 경우의 수를 카운팅 해줘야 한다. [a, b]에서 a=1일 경우로 생각하면 된다. 따라서 현재 answer = 1
3. x=3

x=2일때와 M으로 나눈 나머지가 동일하므로, arr[b]%M == arr[a-1]%M 인 경우이다. (이 때 b는 현재 보고 있는 x값이고, a는 a<=b인 모든 수라고 생각하면 된다.). 따라서 answer = 2가 되고, '2'에서 설명했듯이 [1, 3]또한 0이 되는 경우이므로 answer = 3이 된다.
4. x=4

x=1일 때와 동일하다. 따라서 answer = 4가 된다.
5. x=5

x=2, x=3일 때와 동일하다. 따라서 answer = 6이 된다. 또한 마찬가지로 '2'에서 설명했던 내용에 따라 answer = 7이 된다.
이제 거의 다 왔다. 이제 답을 어떻게 찾을 수 있을지는 알았다. 다만 위에서 예시로 든 것 처럼 매번 M으로 나눈 나머지가 동일한지 찾게 되면 매번 O(N)이 필요하므로, 총 O(N^2)이 필요해서 시간초과가 나게 된다. M의 최대치는 10^3이므로 별도로 cnt[1000] 짜리 배열을 만든 후 이전까지 나왔던 M으로 나눈 나머지의 횟수를 저장해두면 매번 O(1)에 답을 찾을 수 있다. M으로 나눈 나머지를 따로 저장해두는게 아니고, 매번 cnt['M으로로 나눈 나머지']++; 를 해두는 것이다.
while (n-->0) {
int cur = Integer.parseInt(st.nextToken());
sum += cur; // sum은 현재까지의 누적합이다.
sum %= m; // [1, x]의 구간합을 m으로 나눈 나머지 파악
answer += cnt[sum]; // cnt['[1, x]의 구간합을 m으로 나눈 나머지'] 만큼 이전에 동일한 구간합을 m으로 나눈 나머지가 나왔었다.
cnt[sum]++;
if (sum==0) answer++; // '2'에서 설명했던 내용이다.
}
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int sum = 0;
int[] cnt = new int[1000];
long answer = 0;
st = new StringTokenizer(br.readLine());
while (n-->0) {
int cur = Integer.parseInt(st.nextToken());
sum += cur;
sum %= m;
answer += cnt[sum];
cnt[sum]++;
if (sum==0) answer++;
}
System.out.println(answer);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 25756 - 방어율 무시 계산하기 (java) (0) | 2022.10.24 |
|---|---|
| [자바] 백준 11068 - 회문인 수 (java) (0) | 2022.10.21 |
| [자바] 백준 25755 - 거울반사 (java) (0) | 2022.10.20 |
| [자바] 백준 25628 - 햄버거 만들기 (java) (0) | 2022.10.20 |
| [자바] 백준 24263 - 알고리즘 수업 - 알고리즘의 수행 시간 2 (java) (0) | 2022.10.20 |





댓글