목차
※ 배열의 인덱스는 알다시피 0부터 시작한다. 예를들어 N개의 데이터가 있다면 0번 인덱스부터 N-1번 인덱스까지 존재한다. 다만 구현에 있어 누적 합을 구현할 때는 인덱스 1번부터 사용하는게 훨씬 편하다. 즉, N개의 데이터가 존재할 경우, N+1크기의 배열을 만든 후 1번 인덱스부터 N번 인덱스까지를 사용하는게 구현하기 편하다. 따라서 이하 글에서는 후자의 방식을 사용해 서술한다.
※ 코드는 자바 기준으로 작성했지만, 어려운 코드가 아니므로 다른 언어 사용자도 문제없이 볼 수 있어요.
누적 합 (prefix sum)
1. 반복문으로 구간 합을 구할때의 문제점
특정 구간의 합을 구하는 경우를 생각해보자. 예를들어 백준의 구간 합 구하기 4 문제를 보자.

최대 10만개짜리 배열에서, 최대 10만개의 질문에 대해 i번째부터 j번째 까지의 합을 출력해야 한다. N개의 수를 입력받아둔 배열을 arr (N+1개 크기의 배열로 만들고 인덱스 0번은 사용하지 않음)이라고 할 때, 일반적으로 반복문을 사용해 답을 구한다면 다음과 같은 코드가 될 것이다.
int getRangedSum(int[] arr, int i, int j) {
int sum = 0;
for (int idx = i; idx <= j; idx++) {
sum += arr[idx];
}
return sum;
}
1 <= i <= j <= N 이므로, 사실상 위 반복문은 최악의 경우 N번이 돌게되므로 getRangedSum 함수는 O(N)이 필요하다. 그리고 getRangedSum 함수가 총 M번 불릴 것이므로 O(MN) 이라는 시간복잡도가 필요하다. 이 때 N과 M은 모두 최대 100,000이므로 시간 제한인 1초(보통 1억번 정도의 시간복잡도를 가질 시 1초정도로 잡는다. NM은 100억이므로 약 100초가 소요된다.)를 아득히 넘어가게 된다.
2. 더 빠르게 구간합을 구할 방법을 생각해보자
그럼 위에서 살펴본 문제점을 개선하기 위해 속도를 빠르게 해볼 방법을 생각해보자. f(x)를 배열에서 1번째부터 x번째까지의 합이라고 해보자. 즉 위 설명에서 i는 1로 고정하고, j=x이다. 그리고 배열 arr의 i번째 수 arr[i]를 Ai 라고 하겠다. 수식으로 나타내면 아래와 같다.

그럼 이 때 배열 arr에서 a번째부터 b번째까지(a<=b) 구간의 합을 f(x)를 가지고 구할 수 있을까? 우리가 알고자 하는 값은 다음과 같다.
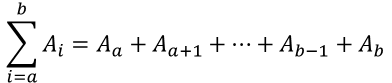
이 때 f(b)와 f(a-1)을 한번 봐보자.

a<=b 이므로 f(b)의 중간에 Aa가 들어가게 된다. 그렇다면 f(b) - f(a-1)은 다음과 같고, 그건 우리가 알고싶은 a번째부터 b번째까지의 구간 합이 된다.

즉, a번째부터 b번째 까지의 구간합을 알기 위해 '1'에서는 Aa, Aa+1, Aa+2, ... , Ab 를 모두 알아야 했고 최악의 경우 N가지를 알아야 가능했지만, 이제는 f(b)와 f(a-1) 두가지만 알면 구할 수 있게 되었다. 즉, O(N)에서 O(2)=O(1)로 줄어들게 된다. 선형에서 상수시간으로 줄어든 것으로 엄청나게 줄어든 것이다.
3. 1부터 x까지의 합은 어떻게 구할까?
그럼 이제 '2'에서 설명했던 1번째부터 x번째까지의 합인 f(x)만 유효한 시간복잡도로 구할 수 있다면 '1'의 문제점을 해결할 수 있다. f(x)는 사실 아래 식만 이해했다면 엄청 간단하게 구할 수 있다. 즉, 1부터 x까지의 합(f(x))은 1부터 x-1까지의 합에 Ax를 더한 값임이 당연하다.
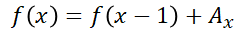
f(x)를 이번엔 prefixSum[x]라고 바꿔서 부르겠다. 그럼 기존에 입력받은 배열 arr[]에 대해 아래와 같이 구해주면 된다. f(x)에 해당하는건 prefixSum[x]에 들어있는 값이 된다.
int[] getPrefixSum(int N, int[] arr) {
int[] prefixSum = new int[N+1];
for (int i = 1; i <= N; i++) {
prefixSum[i] = prefixSum[i-1] + arr[i];
}
return prefixSum;
}

만약 기존 값이 딱히 필요 없다면 다음과 같이 메모리도 추가로 쓰지 않고 계산해줄 수도 있다. 이 경우엔 f(x)에 해당하는게 arr[x]가 된다.
void initPrefixSum(int N, int[] arr) {
for (int i = 1; i <= N; i++) {
arr[i] += arr[i-1];
}
}
4. 구간 합을 사용해 문제를 풀어보자.
위에서 예시로 사용했던 백준의 구간 합 구하기 4 문제를 이번엔 '2~3'에서 설명한 방식대로 한번 코드를 짜봤다. 여기서 nextInt()는 다음 정수를 입력받음을 뜻한다.
// N개의 수를 입력받아 배열에 저장하면서 prefixSum도 함께 만든다.
int[] arr = new int[N+1];
for (int i = 1; i <= N; i++) {
int num = nextInt();
arr[i] = arr[i-1] + num;
}
// a와 b를 입력받아 a번째부터 b번째까지의 합을 구해 answer[]에 담는다.
int[] answer = new int[M+1];
for (int i = 0; i < M; i++) {
int a = nextInt();
int b = nextInt();
answer[i] = arr[b] - arr[a-1];
}
시간 복잡도가 얼마나 차이나는지 살펴보자. 우선 '1'에서와 같이 누적 합을 사용하지 않은 경우엔 O(NM)이었다. 입력받는 시간까지 치면 O(N+NM)이다. 그리고 위 코드와 같이 누적 합을 사용한 경우엔 코드에서 보다시피 O(N+M)이 된다. N과 M이 둘다 최대 100,000 이었으므로 단순 수치로 따지면 O(N+NM)=약 O(10^10), O(N+M)=O(2*10^5) 으로 엄청난 차이를 보이게 된다. 여기서 손해를 본건 없다. 만약 기존 arr 배열 외에 추가로 prefixSum 배열을 두었다면 공간복잡도에서 손해를 보게 되겠으나, 이 문제의 경우엔 입력으로 들어온 배열 자체는 이후 필요가 없으므로 바로 arr에 누적합을 계산해줘서 이득만 봤다.
맨 처음에 얘기한 바와 같이 인덱스는 원래 0부터 시작하는데, 굳이 1번부터 입력받은 이유도 코드에서 볼 수 있다. 인덱스 0번부터 데이터를 받아 사용하려면 arr[i] = arr[i-1] + num; 부분이나 answer[i] = arr[b] - arr[a-1]; 부분에서 i-1과 a-1이 0 이하일 경우를 별도로 처리해줘야 하므로 한마디로 귀찮아진다.
2차원 누적 합 (prefix sum of matrix)
1. 누적합으로 2차원 배열 누적합 구할때의 문제점
RxC 크기의 2차원 배열을 생각해보자.

여기서 이번엔 2차원으로 (1, 3)부터 (2,4)까지의 합과 같이 질문이 들어온다고 하자. (-3-2-3+1 = -7)

R이 최대 1만, C의 최대도 1만, 질문의 개수 Q는 최대 10만이라고 해보자. 이 경우 '누적 합' 설명에서 '1'과 같이 시간 복잡도는 O(RC+QRC)=O(QRC)가 되므로 10^13이나 된다(처음 RC는 입력받는시간, 이후 Q개에 대해 RC번의 2중 반복문). 하지만 우린 이제 누적합 알고리즘을 쓸줄아니깐 각 행별로 누적합을 적용해서 생각해보자. 그럼 (1, 3)부터 (2,4)까지의 합은 (prefixSum[1][4] - prefixSum[1][3-1]) + (prefixSum[2][4] - prefixSum[2][3-1])과 같이 가능하다.

그렇게 해주면 O(RC+QR)=O(QR)로 줄어든다! 만약 시간복잡도가 그정도로도 충분히 통과되는 문제라면 이렇게 해줘도 상관없다. 하지만 이 설명에서는 Q는 10만, R은 1만 이므로 10^9로 1초 이내에 통과할 수 없다.
2. 2차원 누적합으로 2차원 배열을 풀어보자.
실은 좀만 생각해보면 더 빠르게 풀 수 있는 방법이 있다. prefixSum의 규칙을 좀 바꾸는거다. 1차원 배열에서 prefixSum[x]는 1번째부터 x번째까지의 합을 나타냈다. 그럼 이번엔 prefixSum[x][y]를 (1,1)부터 (x,y)까지의 합이라고 해보자.
그럼 prefixSum[x][y]를 만들었다면, 그림(그림은 입력으로 들어온 값을 나타낸다. 즉 arr[][]이다. 또한 마찬가지로 인덱스는 1번부터 사용하도록 했다.)의 빨간 부분 (3, 3)부터 (5, 5)의 합을 어떻게 구할 수 있을까? prefixSum[5][5]는 (1,1)부터 (5,5)까지의 합을 나타내므로 해당 부분에서 저 녹색 부분(prefixSum[2,5])을 빼주고, 노란 부분(prefixSum[5][2])을 빼주고, 두번 빠진 녹색과 노란색이 만나는 부분(prefixSum[2][2])를 한번 더 더해주면 될 것이다.

즉, (3,3)부터 (5,5)까지의 2차원 구간합 = prefixSum[5][5] - prefixSum[5][3-1] - prefixSum[3-1][5] + prefixSum[3-1][3-1] = 36 이다. 모든 경우에 적용될 수 있도록 (x1, y1)부터 (x2, y2) 까지(x1<=x2, y1<=y2)라고 보면 구하고자 하는 2차원 구간합은 다음과 같다.

그럼 (1,1)부터 (x,y)까지의 모든 위치의 값만 유효한 시간내에 구할 수 있다면 그 이후로는 O(1)로 구간합을 구할 수 있음을 알 수 있다.
3. (1,1)부터 (x,y)까지의 합은 어떻게 구할까?
1차원 누적합때와 마찬가지로 이번에도 (1,1)부터 (x,y)까지의 합을 유효한 시간 내에 구하는 방법을 생각해보자. 사실 '2'의 내용을 이해했다면 이건 그 반대로 구하면 된다. 입력으로 들어온 값인 arr[][] 그림을 보자. 저기서 빨간 글자 부분(4,4)에 해당하는 prefixSum[4][4]는 prefixSum[4-1][4] + prefixSum[4][4-1] - prefixSum[4-1][4-1] + arr[4][4]로 구할 수 있다. 즉, 녹색부분과 파란 부분의 누적합을 더하고, 겹치는 부분은 두번 더해졌으므로 한번 빼주고, 현재 값을 더해주면 된다.

RxC 크기의 배열을 입력받았을 때를 기준으로 코드는 다음과 같다.
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= c; j++) {
prefixSum[i][j] = prefixSum[i-1][j] + prefixSum[i][j-1] - prefixSum[i-1][j-1] + arr[i][j];
}
}
마찬가지로 prefixSum 배열을 추가로 만들지 않고, 기존 arr 배열의 값이 이후 필요가 없다면 arr에 바로 만들어도 된다. 코드로는 다음과 같다.
for (int i = 1; i <= r; i++) {
for (int j = 1; j <= c; j++) {
arr[i][j] += arr[i-1][j] + arr[i][j-1] - arr[i-1][j-1];
}
}
arr에서 바로 prefix sum을 구하는 과정을 보자. 파란선 A->B은 B+=A를 뜻한다. 주황선 A->B는 B-=A를 뜻한다.


그럼 이제 원하는 2차원 누적합을 O(1)에 구해볼 수 있다! 예를들어 (2,2) 부터 (5,3)의 구간합을 구해보자. 좌측 arr 배열에서 직접 구하려면 2+3+2+3+2+3+2+3 = 20 이다. 우측 prefixSum에서 구하려면 30-6-5+1 = 20이다.

최종적으로 시간복잡도는 다음과 같다.
A. 2차원 구간의 합을 직접 for문을 돌려 구하는 경우 = O(RC+QRC)
B. 1차원 누적합을 각 행마다 계산하는 경우 = O(RC+QR)
C. 2차원 누적합 사용 = O(RC+Q)
입력받으면서 바로 prefixSum도 만들 수 있으므로 셋에 동일하게 존재하는 O(RC)부분을 제외하면 O(QRC)에서 O(Q)로 줄어든 셈이다.
주의점 및 관련 문제들
1. prefix sum 알고리즘 사용 시 주의점
arr[N]의 값은 결국 입력으로 주어진 모든 수의 합이 된다. 따라서 자료형에 따른 오버플로우를 주의해야한다(음수 표현범위 이하로 내려가는 것도 오버플로우). 예를들어 이 글에서 예시로 들었던 '구간 합 구하기 4' 문제의 경우 N은 최대 10^5이고, 각 값은 최대 1000 이므로, 모두 합쳐봐야 최대 10^8이라서 int 자료형으로 표현해도 아무런 문제가 없었다. 이처럼 최대값을 생각해보고 자료형을 구해 누적합을 계산해줘야 한다. 만약 누적합 알고리즘을 정말 쓰고 싶은데 최대치가 자료형의 범위를 넘어간다면 보통 누적합으로 푸는 문젠 아닐꺼다. 출제자가 변태가 아닌 이상 분명 그렇겐 안낸다. 누적합 밖에 풀 방법이 생각이 안난다면 각 언어에 있는 큰 수 자료형을 쓰거나 그냥 정신건강상 파이썬
2. 풀어볼만한 PS 문제들
[ 기본 ]
백준 11659 : 구간 합 구하기 4
누적합 기본 문제이다.
백준 17390 : 이건 꼭 풀어야 해!
위 문제에서 정렬이 추가되서 아주 약간 응용되었다.
백준 11660 : 구간 합 구하기 5
누적합을 행이나 열의 수 만큼 적용해도 되고, 2차원 누적합으로 풀어도 되는 문제이다. 둘 다 한번 구현해보자.
[ 응용 ]
백준 10986 : 나머지 합
누적합 응용버전이다. 한번 풀어보자.
백준 17425 : 약수의 합
누적합은 거들뿐..
백준 2143 : 두 배열의 합
위쪽에 적어둔 누가봐도 누적합 쓰면 쉽게 구할 수 있는 문제들과 달리 약간 거드는 느낌으로 자연스레 쓰이는 경우가 많다.
백준 23046 : 큰 수 뒤집기
플2 문제로 많이 어렵다. 누적합인걸 안다고 바로 풀수 있는 문제는 아니다. 간단한 문제뿐 아니라 이런식으로도 누적합을 써먹을 수 있다는 의미로 넣어봤다.
백준 2835 : 인기도 조사
세그먼트 트리 lazy propagation이 생각나는 문제지만, 의외로 누적합으로 풀 수 있긴한데 아마 누적합으로 푸는 방법을 찾긴 힘들 것이다. 풀이를 보면 이왜진 느낌으로 풀 수 있다.
'CS > Algorithms' 카테고리의 다른 글
| 브루트포스 알고리즘 (Brute force 알고리즘) (0) | 2023.03.15 |
|---|---|
| 벡터의 외적과 CCW (Counter ClockWise) (4) | 2022.11.15 |
| 분할 정복을 이용한 거듭제곱 최적화 (0) | 2022.04.05 |
| 에라토스테네스의 체 혹은 소수판정 시 제곱근 까지만 확인하면 되는 이유 (4) | 2022.02.12 |
| 백트래킹 알고리즘 (Back Tracking) (0) | 2021.10.03 |





댓글