목차
문제 : boj11378

필요 알고리즘 개념
- 네트워크 플로우(최대 유량)
- 애드몬드 카프 등의 네트워크 플로우(최대 유량) 알고리즘을 알고 있어야 한다. 단, 자바의 경우 빠른 입출력까지 사용해야 애드몬드 카프 알고리즘으로 시간 초과 없이 통과 가능하다.
- 이분매칭
- 네트워크 플로우에서 이분 그래프로 구성이 가능할 시 사용 가능한 이분매칭 알고리즘을 사용하면 네트워크 플로우보다 더 빠른 시간내에 통과 가능하다. 이 경우엔 자바라도 빠른 입출력 없이도 여유롭게 통과 가능하다.
- 풀이 1과 풀이 2에서 최대 유량을 이용한 풀이를 한다. 풀이 3과 4에서는 이분매칭을 통해 풀어본다. 각 풀이는 네트워크 플로우 또는 이분매칭 알고리즘의 기본적인 구현 방식을 알고있다는 전제하에, k개의 추가된 일을 어떻게 처리하는지에 중점을 두고 작성했다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이 1 : 네트워크 플로우(최대 유량) - 정점 추가 없이, k번은 추가로 돌려서 처리
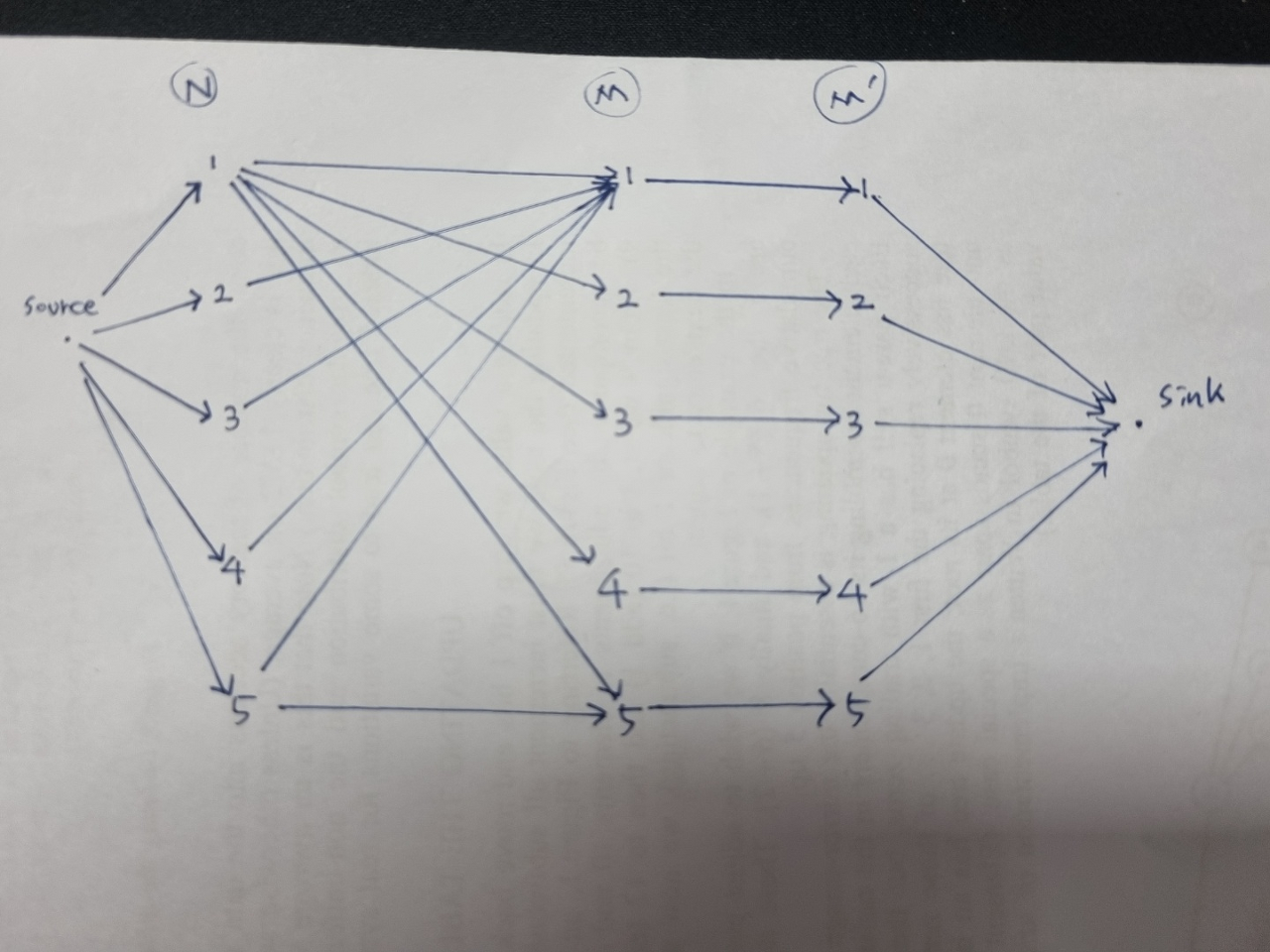
source에서 N개의 사람에게 간선이 가고(유량 1), N에서 M개의 일로 가능한 일에 대해 간선을 그어준다(유량 1). 그리고 M에서 M'은 M이 1개만 가능하기 때문에 만들어줬는데, 풀이를 쓰다보니 어차피 sink로 유량 1로 떨어질테니 M'은 필요없다. 최대 유량에 아직 익숙하지 않아서 쓸데없는 간선을 추가로 그리게 됬다. 아무튼 M에서 sink로 마찬가지로 유량 1짜리 간선을 그려준다. 즉, 위 그래프에서 모든 유량은 1이다.
이대로 우선 에드몬드 카프 알고리즘을 돌려서 기본적으로 가능한 일의 수를 계산해준다(코드의 [A]). 그리고, k가 0보다 큰 동안 source에서 각 N개의 사람한테 가는 간선한테 각각 남아 있는 k만큼의 유량을 추가한 후 돌려주면서 k에 대한 처리를 해준다(코드의 [B]).
코드 (풀이 1) : github
private void solution() throws Exception {
int n = nextInt();
int m = nextInt();
int k = nextInt();
int source = 0;
int sink = n+m+m+1;
int len = sink+1;
int[][] capacity = new int[len][len];
int[][] flow = new int[len][len];
ArrayList<Integer>[] edges = new ArrayList[len];
for (int i = 0; i < len; i++) edges[i] = new ArrayList<>();
// source to N
for (int i = 1; i <= n; i++) {
capacity[source][i] = 1;
edges[source].add(i);
edges[i].add(source);
}
// N to M
for (int i = 1; i <= n; i++) {
int a = nextInt();
while (a-->0) {
int tmp = nextInt();
capacity[i][tmp+n] = 1;
edges[i].add(tmp+n);
edges[tmp+n].add(i);
}
}
// M to M'
for (int i = n+1; i <= n+m; i++) {
capacity[i][i+m] = 1;
edges[i].add(i+m);
edges[i+m].add(i);
}
// M' to sink
for (int i = n+m+1; i <= n+m+m; i++) {
capacity[i][sink] = 1;
edges[i].add(sink);
edges[sink].add(i);
}
// solution
int sum = 0;
// [A]
while (true) {
int[] parents = new int[len];
Arrays.fill(parents, -1);
Queue<Integer> q = new ArrayDeque<>();
q.add(source);
parents[source] = source;
while (!q.isEmpty() && parents[sink] == -1) {
int cur = q.poll();
for (int next : edges[cur]) {
if (parents[next] == -1 && capacity[cur][next] - flow[cur][next] > 0) {
parents[next] = cur;
q.add(next);
}
}
}
if (parents[sink] == -1) break;
int min = Integer.MAX_VALUE;
for (int i = sink; i != source; i = parents[i]) {
min = Math.min(min, capacity[parents[i]][i] - flow[parents[i]][i]);
}
for (int i = sink; i != source; i = parents[i]) {
flow[parents[i]][i] += min;
flow[i][parents[i]] -= min;
}
sum += min;
}
// [B]
for (int x = 1; x <= n && sum < m && k > 0; x++) {
capacity[0][x] += k;
int sumTmp = 0;
while (true) {
int[] parents = new int[len];
Arrays.fill(parents, -1);
Queue<Integer> q = new ArrayDeque<>();
q.add(source);
parents[source] = source;
while (!q.isEmpty() && parents[sink] == -1) {
int cur = q.poll();
for (int next : edges[cur]) {
if (parents[next] == -1 && capacity[cur][next] - flow[cur][next] > 0) {
parents[next] = cur;
q.add(next);
}
}
}
if (parents[sink] == -1) break;
int min = Integer.MAX_VALUE;
for (int i = sink; i != source; i = parents[i]) {
min = Math.min(min, capacity[parents[i]][i] - flow[parents[i]][i]);
}
for (int i = sink; i != source; i = parents[i]) {
flow[parents[i]][i] += min;
flow[i][parents[i]] -= min;
}
sumTmp += min;
}
sum += sumTmp;
k -= sumTmp;
}
System.out.println(sum);
}
풀이 2 : 네트워크 플로우(최대 유량) - 정점을 추가하여 한 번의 에드몬드 카프로 해결
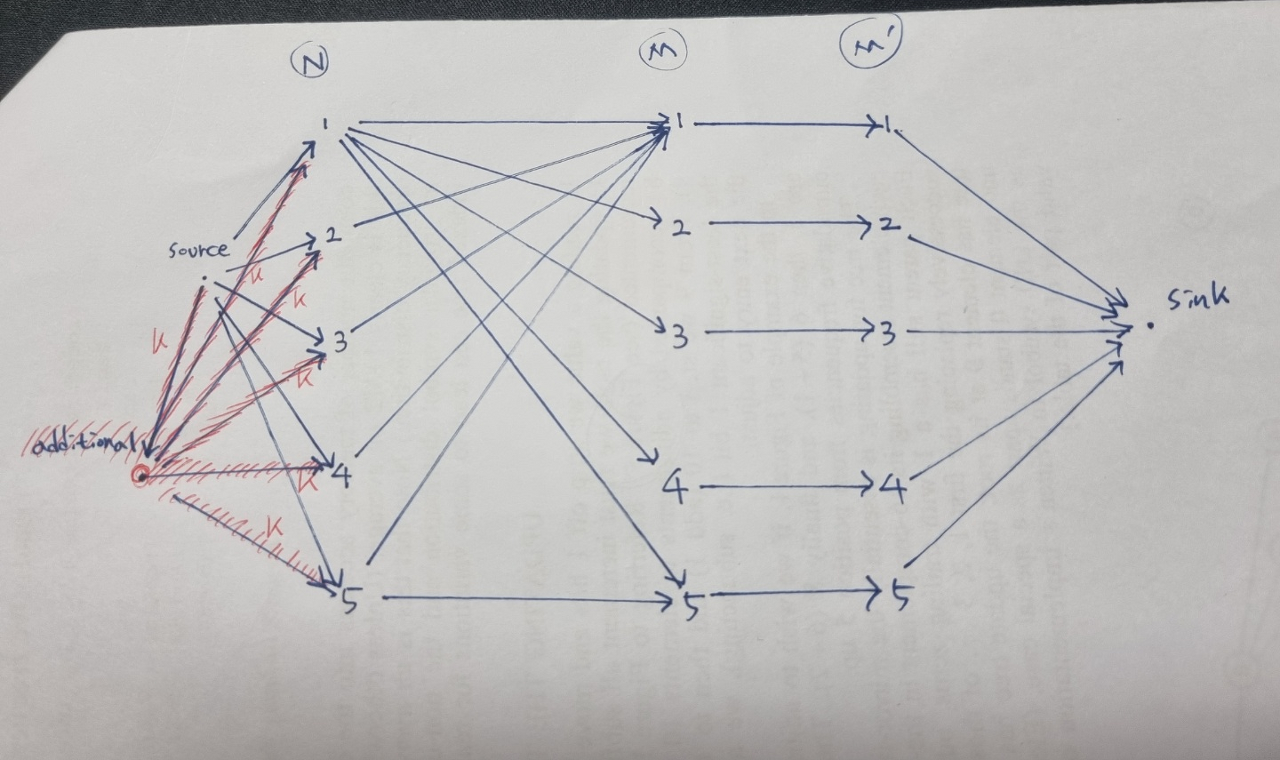
이번엔 풀이 1과 다르게, 정점을 하나 추가해서 k를 처리해보자. source에서 추가 정점으로 유량 k를 가진 간선을 그어주면 k개의 추가 일을 처리할 수 있다. 이 때 주의점은 추가 정점에서 N개의 사람 정점으로 유량이 1이면 안되고 k여야 한다(추가 일을 한 사람이 모두 할 수도 있으므로 그렇다.). 어차피 source에서 추가 정점으로 유량이 k 이므로, 추가 정점에서 N개의 정점으로 k의 유량을 줘도 최대 k로 제한된다. 그림상에서 빨간색 배경 부분이 추가된 정점 및 유량이다.
풀이 1과 마찬가지로 M'은 내가 아직 네트워크 플로우를 익히는 단계라 쓸데없이 추가된 부분으로 풀이를 쓰다보니 필요없음을 깨달아 삭제하지 못했다. M 정점들에서 바로 sink로 이어주면 된다.
위처럼 흐름을 설계할 시, 풀이 1과는 다르게 추가적인 구현 필요 없이 에드몬드 카프 알고리즘을 한번만 돌려주면 된다.
코드 (풀이 2) : github
private void solution() throws Exception {
int n = nextInt();
int m = nextInt();
int k = nextInt();
int source = 0;
int sink = n+m+m+1;
int additional = sink+1;
int len = sink+2;
int[][] capacity = new int[len][len];
int[][] flow = new int[len][len];
ArrayList<Integer>[] edges = new ArrayList[len];
for (int i = 0; i < len; i++) edges[i] = new ArrayList<>();
// source to N
for (int i = 1; i <= n; i++) {
capacity[source][i] = 1;
edges[source].add(i);
edges[i].add(source);
}
// additional node
capacity[source][additional] = k;
edges[source].add(additional);
edges[additional].add(source);
// additional node to N
for (int i = 1; i <= n; i++) {
capacity[additional][i] = k;
edges[additional].add(i);
edges[i].add(additional);
}
// N to M
for (int i = 1; i <= n; i++) {
int a = nextInt();
while (a-->0) {
int tmp = nextInt();
capacity[i][tmp+n] = 1;
edges[i].add(tmp+n);
edges[tmp+n].add(i);
}
}
// M to M'
for (int i = n+1; i <= n+m; i++) {
capacity[i][i+m] = 1;
edges[i].add(i+m);
edges[i+m].add(i);
}
// M' to sink
for (int i = n+m+1; i <= n+m+m; i++) {
capacity[i][sink] = 1;
edges[i].add(sink);
edges[sink].add(i);
}
// solution
int sum = 0;
while (true) {
int[] parents = new int[len];
Arrays.fill(parents, -1);
Queue<Integer> q = new ArrayDeque<>();
q.add(source);
parents[source] = source;
while (!q.isEmpty() && parents[sink] == -1) {
int cur = q.poll();
for (int next : edges[cur]) {
if (parents[next] == -1 && capacity[cur][next] - flow[cur][next] > 0) {
parents[next] = cur;
q.add(next);
}
}
}
if (parents[sink] == -1) break;
int min = Integer.MAX_VALUE;
for (int i = sink; i != source; i = parents[i]) {
min = Math.min(min, capacity[parents[i]][i] - flow[parents[i]][i]);
}
for (int i = sink; i != source; i = parents[i]) {
flow[parents[i]][i] += min;
flow[i][parents[i]] -= min;
}
sum += min;
}
System.out.println(sum);
}
풀이 3 : 이분 매칭 - 정점 추가 없이, k번은 추가로 돌려서 처리

N과 M 사이에 이분그래프를 만들어줄 수 있으므로, 이분매칭 알고리즘으로 풀 수 있다. 시간차이의 경우 최대 유량이 약 5700ms, 이분매칭이 약 600ms로 10배가량 시간차이가 났다(최대 유량을 아직 공부하는 단계이기 때문에 내가 제대로 처리 못했을 수도 있다.).
N에서 M으로의 간선들을 설정해준 후, 우선 이분매칭을 한번 돌려주고(코드의 [A]), k개는 그 이후 k가 0이 되거나 더이상 추가로 매칭되는게 없을 때 까지(코드상으로 tmp==0이면 추가로 찾아지는 매칭이 없는 경우) 이분매칭을 더 돌려주면 된다.
코드 (풀이 3) : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
int[] matched;
boolean[] v;
int[][] edges;
private boolean matching(int cur) {
for (int i = 0; i < edges[cur].length; i++) {
int next = edges[cur][i];
if (v[next]) continue;
v[next] = true;
if (matched[next] == -1 || matching(matched[next])) {
matched[next] = cur;
return true;
}
}
return false;
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
matched = new int[m+1];
Arrays.fill(matched, -1);
v = new boolean[m+1];
edges = new int[n+1][];
for (int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
edges[i] = new int[a];
for (int j = 0; j < a; j++) {
edges[i][j] = Integer.parseInt(st.nextToken());
}
}
int sum = 0;
// [A]
for (int i = 1; i <= n && sum < m; i++) {
if (matching(i)) {
sum++;
v = new boolean[m+1];
}
}
// [B]
while (true) {
int tmp = 0;
for (int i = 1; i <= n && sum < m && k > 0; i++) {
if (matching(i)) {
tmp++;
k--;
v = new boolean[m+1];
}
}
sum += tmp;
if (tmp == 0 || sum >= m || k == 0)
break;
}
System.out.println(sum);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}
풀이 4 : 이분 매칭 - k개의 정점을 추가해서 추가 구현 없이 k번의 일을 처리
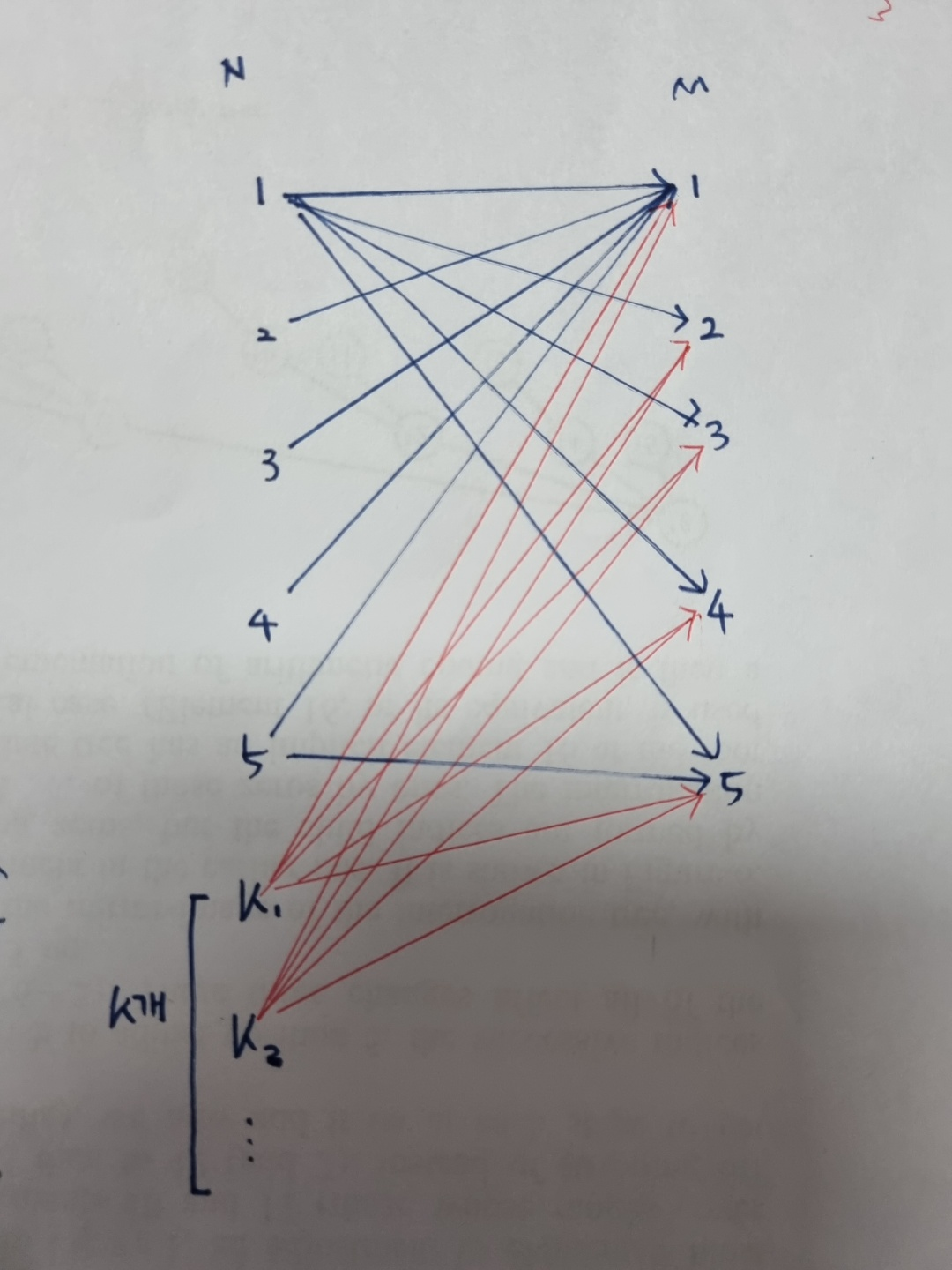
위의 방식들로 풀고나서 '난이도 기여'에 있는 aym506님의 "K개의 정점을 추가해서 이분 매칭을 시도하거나" 라는 멘트를 봤다. 좋은 아이디어 같아서 시도해보려고 했는데, 내 생각엔 k개의 추가 정점들은 M개의 일들한테 모두 간선을 그어주면 될 것 같았는데, 틀렸다고 떠서 감이 잘 안왔었다.
기초적인 실수였는데, 당연하게도 M이 10이라고 해서 모든 10개의 정점에게 N -> M으로의 간선이 존재하는 것은 아니다. 예를들어 위 그림에서 M이 6개였다면 6번째 정점으로는 아무런 간선도 발생하지 않았을 것이다. 그러므로 k개의 추가정점에서는 한번이라도 입력이 들어왔던 모든 일의 번호로만 간선을 이어줘야 한다. 해당 부분은 해시셋을 통해 처리할 수 있다(코드상 fullEdge 참고).
코드 (풀이 4) : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.HashSet;
import java.util.StringTokenizer;
public class Main {
int[] matched;
boolean[] v;
int[][] edges;
int[] fullEdge;
int n;
private boolean matching(int cur) {
int[] edge = cur <= n ? edges[cur] : fullEdge;
for (int next : edge) {
if (v[next]) continue;
v[next] = true;
if (matched[next] == -1 || matching(matched[next])) {
matched[next] = cur;
return true;
}
}
return false;
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
matched = new int[m+1];
Arrays.fill(matched, -1);
v = new boolean[m+1];
edges = new int[n+1][];
HashSet<Integer> hs = new HashSet<>();
for (int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
edges[i] = new int[a];
for (int j = 0; j < a; j++) {
hs.add(edges[i][j] = Integer.parseInt(st.nextToken()));
}
}
fullEdge = new int[hs.size()];
int idx = 0;
for (int i = 0; i < m; i++) {
if (hs.contains(i+1))
fullEdge[idx++] = i+1;
}
int sum = 0;
for (int i = 1; i < n+k+1 && sum < m; i++) {
if (matching(i)) {
sum++;
v = new boolean[m+1];
}
}
System.out.println(sum);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}
'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 26209 - Intercepting Information (java) (0) | 2022.12.21 |
|---|---|
| [자바] 백준 8545 - Zadanie próbne (java) (0) | 2022.12.21 |
| [자바] 백준 25822 - 2000문제 푼 임스 (java) (0) | 2022.12.15 |
| [자바] 백준 24078 - Remainder (java) (0) | 2022.12.13 |
| [자바] 백준 1981 - 배열에서 이동 (java) (0) | 2022.12.13 |





댓글