목차
문제 : boj1688

필요 알고리즘
- 오목 다각형 내부의 점 판정
- 딱히 어려운 부분은 아니다. 선분 교차 판정의 응용으로, 풀이를 보면 어떻게 판정하는지 바로 알 수 있다.
- 기하학, CCW, 선분 교차 판정
- CCW를 이용한 선분 교차 판정을 통해 오목 다각형 내부의 점을 판정하는 문제이다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
우선 CCW와 선분 교차 판정을 모르면 구현이 불가하다. 모른다면 이하 글을 참고해보자.
- CCW : 벡터의 외적과 CCW (Counter ClockWise)
- 선분 교차 판정 : CCW를 이용한 선분 교차 여부 판정
선분 교차 판정을 안다면 오목 다각형 내부의 점 판정은 그리 어렵지 않은데, 그냥 외부 무한대 위치로(입력값 최대치 이상) 선을 쭉 그어서 선분 교차판정을 한 결과가 홀수면 오목 다각형 내부에 있는거다. 이하 이미지에서 다각형 내부의 파란 점들은 외부로 어디로 선을 긋든 홀수개 위치에서 만나고, 다각형 외부의 빨간 점은 짝수개 위치에서 만나는걸 확인할 수 있다.
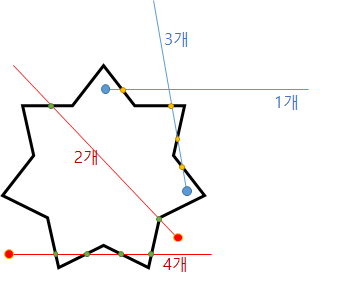
친절하게도(?) 문제에서 꼭짓점들의 좌표를 '순서대로' 주므로, 순서대로 선을 만들어 생성되는 모든 선을 위처럼 외부 무한대 방향으로 그은 선과 선분 교차판정을 하면 몇 개의 선과 교차되는지 확인할 수 있다.
주의점은 '다각형 경계위에 있는 경우에는 보호되는 것' 라고 했으므로 추가로 확인할게 있다. 추가로 확인할 부분을 포함한 전체로직은 다음과 같다.
1. 주어진 점과 대연, 영훈, 범진의 좌표중 동일한 값이 있다면 1을 출력하고 종료한다. (코드의 samePointExist()) -> 점들끼리 x, y 좌표가 동일한지만 보면 된다.
2. 입력된 점들로 만들어진 선 위에 대연, 영훈, 범진의 좌표가 올라간다면 1을 출력하고 종료한다. (코드의 curPointIsOnLine()) -> (x,y)에서 (x,y)로의 선은 길이는 없지만 아무튼 선이다. 동일하게 선분 교차 판정을 할 수 있다.
3. 대연, 영훈, 범진의 좌표에서 외부 무한대로 그은 선과 입력값들로 만들어진 모든 선을 선분 교차판정해서 교차하는 개수를 센다. 최종적으로 교차하는 지점이 홀수개라면 1, 짝수개라면 0을 출력해주면 된다. (코드의 cnt&1 은 cnt가 홀수일 시 1, 짝수일 시 0이 나온다.) -> 이 때, 외부 무한대로 그은 선이 기존 선과 평행이면 처리하기가 귀찮아지므로 내 경우엔 대충 평행이 되지 않을 만한 값으로 정했다 (x, y) = (1000000001-41, 1000000001).
for (int i = 0; i < 3; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
Point curPoint = new Point(x, y);
// '1'과 '2'의 예외 처리
if (samePointExist(curPoint, points) || curPointIsOnLine(curPoint, lines)) {
sb.append(1).append('\n');
continue;
}
// 이하 '3' 처리
Line cur = new Line(curPoint, new Point(LIMIT-41, LIMIT));
int cnt = 0;
for (Line line : lines) {
if (Line.isIntersection(cur, line)) cnt++;
}
sb.append(cnt&1).append('\n');
}
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private static final int LIMIT = 1000000001;
public static void main(String[] args) throws Exception {
new Main().solution();
}
private void solution() throws Exception {
int n = Integer.parseInt(br.readLine());
Point[] points = new Point[n+1];
for (int i = 1; i <= n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
points[i] = new Point(x, y);
}
points[0] = points[n];
List<Line> lines = new ArrayList<>();
for (int i = 1; i <= n; i++) {
lines.add(new Line(points[i-1], points[i]));
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < 3; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
Point curPoint = new Point(x, y);
if (samePointExist(curPoint, points) || curPointIsOnLine(curPoint, lines)) {
sb.append(1).append('\n');
continue;
}
Line cur = new Line(curPoint, new Point(LIMIT-41, LIMIT));
int cnt = 0;
for (Line line : lines) {
if (Line.isIntersection(cur, line)) cnt++;
}
sb.append(cnt&1).append('\n');
}
System.out.print(sb);
}
private boolean curPointIsOnLine(final Point curPoint, final List<Line> lines) {
Line cur = new Line(curPoint, curPoint);
for (Line line : lines) {
if (Line.isIntersection(cur, line)) {
return true;
}
}
return false;
}
private boolean samePointExist(final Point curPoint, final Point[] points) {
for (Point point : points) {
if (curPoint.equals(point)) {
return true;
}
}
return false;
}
}
class Point implements Comparable<Point> {
long x, y;
public Point(long x, long y) {
this.x = x;
this.y = y;
}
@Override
public boolean equals(final Object obj) {
Point o = (Point) obj;
return this.x == o.x && this.y == o.y;
}
@Override
public int compareTo(Point o) {
if (this.equals(o))
return 0;
if (this.x == o.x)
return this.y-o.y < 0 ? -1 : 1;
return this.x - o.x < 0 ? -1 : 1;
}
}
class Line {
Point p1, p2;
public Line(Point p1, Point p2) {
this.p1 = p1.compareTo(p2)<=0?p1:p2;
this.p2 = p1.compareTo(p2)<=0?p2:p1;
}
public Line(int x1, int y1, int x2, int y2) {
this(new Point(x1, y1), new Point(x2, y2));
}
private static int ccw(Point a, Point b, Point c) {
Point[] arr = {a,b,c,a};
long sum = 0;
for (int i = 0; i < 3; i++) {
sum += 1l*arr[i].x*arr[i+1].y-1l*arr[i+1].x*arr[i].y;
}
return sum>0?1:sum<0?-1:0;
}
public static boolean isIntersection(Line line1, Line line2) {
int res1 = ccw(line1.p1, line1.p2, line2.p1);
int res2 = ccw(line1.p1, line1.p2, line2.p2);
int res3 = ccw(line2.p1, line2.p2, line1.p1);
int res4 = ccw(line2.p1, line2.p2, line1.p2);
if (res1!=res2 && res3!=res4)
return true;
if (res1==0 && res2==0 && res3==0 && res4==0)
return line1.p1.compareTo(line2.p2)<=0 && line2.p1.compareTo(line1.p2)<=0;
return false;
}
}
'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 21278 - 호석이 두 마리 치킨 (java) (0) | 2023.06.13 |
|---|---|
| [자바] 백준 27468 - 2배 또는 0.5배 (java) (0) | 2023.05.15 |
| [자바] 백준 28017 - 게임을 클리어하자 (java) (0) | 2023.05.12 |
| [자바] 백준 14254 - 비밀번호 변경 (java) (0) | 2023.05.11 |
| [자바] 백준 15558 - 점프 게임 (java) (0) | 2023.05.10 |





댓글