업데이트 : 2023-05-12
- 코드 잘못된 부분 수정 ( min(p1,p2) ≤ max(q1,q2) && min(q1,q2) ≤ max(p1,p2) 라고 설명은 잘 적어뒀으나, 올린 코드가 잘못됬었음.)
line1.p1.compareTo(line2.p2)<=0 && line1.p1.compareTo(line1.p2)<=0;
->
line1.p1.compareTo(line2.p2)<=0 && line2.p1.compareTo(line1.p2)<=0;
목차
벡터의 외적과 CCW (Counter ClockWise)에서 이어지는 글 입니다. CCW가 어떤건지 이미 알고 있다면 이 글만 보셔도 이해에 문제는 없습니다.
이하 bold 처리된 대문자 $\textbf{A}, \textbf{B}$는 벡터를 뜻합니다.
CCW
왜 이하와 같이 되는지 자세한 내용은 위에 링크된 '벡터의 외적과 CCW' 글을 참고해주세요.
- 짧게 CCW에 대해 다시 얘기해보자.
- 점 $a=(x_1, y_1, 0), b=(x_2, y_2, 0), c=(x_3, y_3, 0)$ 이라할 때, $\textbf{A}=\vec{ab}=(x_2-x_1, y_2-y_1, 0), \textbf{B}=\vec{ac}=(x_3-x_1, y_3-y_1, 0)$ 이다.
- 따라서 $\textbf{A}\times\textbf{B}=(0, 0, (x_2-x_1)(y_3-y_1)-(y_2-y_1)(x_3-x_1))$ 이다.
- $\left|\textbf{A}\times\textbf{B}\right| = (x_2-x_1)(y_3-y_1)-(y_2-y_1)(x_3-x_1) = x_1y_2+x_3y_3+x_3y_1-(y_1x_2+y_2x_3+y_3x_1)$
- 이 때 $\left|\textbf{A}\times\textbf{B}\right| = D$라고 해보자.
- $D>0$ 이라면 $\textbf{A}$를 기준으로 $\textbf{B}$는 반시계 방향이다.
- $D=0$ 이라면 $\textbf{A}$와 $\textbf{B}$는 평행이다.
- $D<0$ 이라면 $\textbf{A}$를 기준으로 $\textbf{B}$는 시계 방향이다.

선분 교차 판정
- 이후 설명에서 ccw(a,b,c) 는 이하와 같은 로직을 뜻한다.
- 평면상의 점 a, b, c를 순서대로 입력받아 두 벡터 $\textbf{A}, \textbf{B}$ 를 이하와 같이 정의한다.
- $\textbf{A}=\vec{ab}=(b.x-a.x, b.y-b.x, 0)$
- $\textbf{B}=\vec{ac}=(c.x-a.x, c.y-c.x, 0)$
- $\left|\textbf{A}\times\textbf{B}\right| = D$
- 이 때, $D>0$이면 return 1, $D<0$이면 return -1, $D=0$이면 return 0을 하는 함수이다.
코드로 나타내면 다음과 같다.
// Point는 평면상의 점을 뜻한다. 따라서 z축은 0이므로 따로 받지 않는다.
class Point {
int x, y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
---
// 신발끈 공식을 사용한 ccw 구현
public int ccw(Point a, Point b, Point c) {
Point[] arr = {a,b,c,a};
long sum = 0;
for (int i = 0; i < 3; i++) {
sum += arr[i].x*arr[i+1].y-arr[i+1].x*arr[i].y;
}
return sum>0?1:sum<0?-1:0;
}
---
// 글에 제시된 공식 중 하나를 사용한 ccw 구현1
public int ccw(Point a, Point b, Point c) {
long sum = 1l*(b.x-a.x)*(c.y-a.y)-1l*(b.y-a.y)*(c.x-a.x);
if (sum>0) return 1;
if (sum<0) return -1;
return 0;
}
---
// 글에 제시된 공식 중 하나를 사용한 ccw 구현2
public int ccw(Point a, Point b, Point c) {
long sum = 1l*a.x*b.y + 1l*b.x*c.y + 1l*c.x*a.y - (1l*a.y*b.x + 1l*b.y*c.a + 1l*c.y*a.x);
if (sum>0) return 1;
if (sum<0) return -1;
return 0;
}
예를들어 아래 좌측 이미지를 보자. 여기서 ccw(p1,p2,q1) 은 우측 이미지처럼 생각하면 된다. $\textbf{A}$를 기준으로 $\textbf{B}$는 반시계 방향이므로 -1이 리턴될 것이다.

- 이 글에서 알고싶은건 두 선분(벡터)이 주어졌을 때 두 선분이 교차하는지 판정하는 것이다.
어떻게 선분이 교차하는지 알 수 있을까? 현재 이 글에서 가진 도구는 CCW이다. 이건 세 점의 방향 관계를 -1, 0, 1 과 같이 나타내주는 알고리즘(수식)이다.
당연히 교차해보이는 [1]을 보자. 이 때, ccw(p1,p2,q1), ccw(p1,p2,q2) 결과는 [2]와 같을 것이다. 한 선분에서 다른 선분의 두 점으로의 결과가 하나는 반시계, 하나는 시계방향이라면 기준이 된 선분이 그 사이에 있을 것으로 생각해볼 수 있다.

하지만 [3]을 보면 그것만 가지곤 부족함을 알 수 있다.
따라서 [4]와 같이 선분1에서 선분2의 두 점으로의 ccw 결과과 달라야 하고, 선분2에서 선분1의 두 점으로의 ccw 결과또한 달라야 교차함을 알 수 있다. [3]에서 봤던 예외사항도 [5]와같이 한쪽은 결과가 다른데, 한쪽은 결과가 동일하므로 교차하지 않음을 알 수 있다.
- 다른 경우도 살펴보자.

모두 위에서 말한 방식대로 교차 판정이 가능함을 확인할 수 있다. [6], [7], [8]은 교차하고, [9]는 교차하지 않는다.
- 예외가 존재한다.
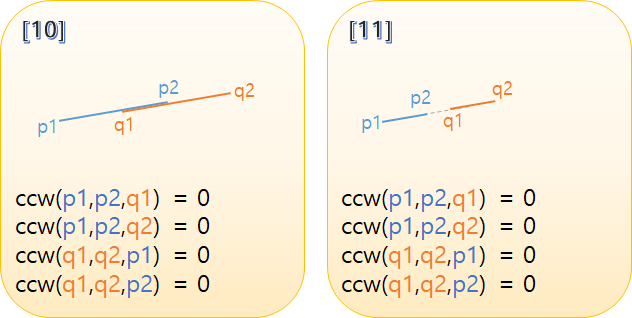
[10](그림으로는 어긋나보이지만, 일직선으로 겹쳐있는 경우이다.)과 [11]의 경우 두 경우 모두 모든 ccw 값이 0이다.
하지만 [10]은 교차한 경우이므로 별도로 처리해줘야 한다.
각 점에 대해 대소관계를 '좌측 상단에 있을 수록 작은 것, 우측 하단에 있을 수록 큰 것'처럼 규칙을 정해보자. 이 경우 대소관계 규칙은 어떻게 정하든 상관없다. 하나의 프로그램에서 규칙이 바뀌지만 않으면 된다. 코드로 규칙을 구현해보면 아래와 같다.
class Point implements Comparable<Point> {
int x, y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
@Override
public int compareTo(Point o) {
if (this.x == o.x)
return this.y-o.y;
return this.x-o.x;
}
}
그럼 정한 대소관계 규칙에 따라 [10]의 경우 min(p1,p2) ≤ max(q1,q2) && min(q1,q2) ≤ max(p1,p2) 라면 교차함을 판단할 수 있다. 그럼 이제 코드로 살펴보자.
선분 교차 판정 코드
Line의 생성자에서 이미 p1<=p2 임이 보장된다. 따라서 위에서 설명한 min, max 부분은 별도로 없다. 교차 판정 코드1과 교차 판정 코드2를 봐보자. 둘 다 위에서 나온 케이스들을 판정해준다. 설명의 흐름대로 따라가려면 교차 판정 코드 1을 보면 된다. 다만 코드가 좀 긴 편이라, 교차 판정 코드 2로 변경해서 사용해도 된다. 어차피 모든 케이스를 살펴봤으므로 어쨌든 결과만 만족하도록 짜면 된다.
class Point implements Comparable<Point> {
int x, y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
@Override
public int compareTo(Point o) {
if (this.x == o.x)
return this.y-o.y;
return this.x-o.x;
}
}
class Line {
Point p1, p2;
public Line(Point p1, Point p2) {
this.p1 = p1.compareTo(p2)<=0?p1:p2;
this.p2 = p1.compareTo(p2)<=0?p2:p1;
}
public Line(int x1, int y1, int x2, int y2) {
this(new Point(x1, y1), new Point(x2, y2));
}
private int ccw(Point a, Point b, Point c) {
Point[] arr = {a,b,c,a};
long sum = 0;
for (int i = 0; i < 3; i++) {
sum += 1l*arr[i].x*arr[i+1].y-1l*arr[i+1].x*arr[i].y;
}
return sum>0?1:sum<0?-1:0;
}
// 교차 판정 코드 1
public boolean isIntersection(Line line1, Line line2) {
// [A] line1에서 line2의 두 점으로의 ccw 계산
int res1 = ccw(line1.p1, line1.p2, line2.p1);
int res2 = ccw(line1.p1, line1.p2, line2.p2);
// [B] line2에서 line1의 두 점으로의 ccw 계산
int res3 = ccw(line2.p1, line2.p2, line1.p1);
int res4 = ccw(line2.p1, line2.p2, line1.p2);
// [A]의 두 값이 다르고, [B]의 두 값도 다르다면 교차한다. ([1]~[9] 판단)
if (res1!=res2 && res3!=res4)
return true;
// [A]와 [B]에서 계산한 ccw 4개가 전부 0이라면 예외케이스로 판단해준다. ([10], [11] 판단)
if (res1==0 && res2==0 && res3==0 && res4==0)
return line1.p1.compareTo(line2.p2)<=0 && line2.p1.compareTo(line1.p2)<=0;
return false;
}
// 교차 판정 코드 2
public boolean isIntersection2(Line line1, Line line2) {
// [C] line1에서 line2의 두 점으로의 ccw를 미리 곱해준다.
int res1 = ccw(line1.p1, line1.p2, line2.p1) * ccw(line1.p1, line1.p2, line2.p2);
// [D] line2에서 line1의 두 점으로의 ccw를 미리 곱해준다.
int res2 = ccw(line2.p1, line2.p2, line1.p1) * ccw(line2.p1, line2.p2, line1.p2);
// [C]와 [D]가 둘 다 0이 되는 경우는 [8], [10], [11]의 경우이다. 두 경우 모두 대소관계로 판단 가능하다.
if (res1 == 0 && res2 == 0) {
return line1.p1.compareTo(line2.p2)<=0 && line2.p1.compareTo(line1.p2)<=0;
}
// 나머지 경우는 모두 이하로 판단 가능하다.
return res1<=0 && res2<=0;
}
}
관련 알고리즘 문제
위에 나온 설명 그대로 구현하면 된다. 이 때, '세 점이 일직선 위에 있는 경우는 없다.' 라는 지문에 따라 예외 사항을 체크하지 않아도 되는 문제이다.
'선분 교차 1'에서 예외 사항도 추가된 버전이다.
위의 두 문제는 너무 대놓고 선분 교차 판정을 하라고 써있다. 물론 이 문제도 비슷하긴 한데, 어쨌든 좀 더 실제로 있을법한 문제이다.
최대 3000개의 선분들에 대한 교차 판정을 해줘야 한다. 선분 교차 판정 알고리즘에 더해서 분리 집합 알고리즘도 알고 있다면 좀 더 편하게 풀 수 있는데, 없어도 풀 순 있다.
References
https://www.geeksforgeeks.org/check-if-two-given-line-segments-intersect/
How to check if two given line segments intersect? - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
https://gaussian37.github.io/math-algorithm-line_intersection/
선분의 교차 여부 확인
gaussian37's blog
gaussian37.github.io
https://bryceboe.com/2006/10/23/line-segment-intersection-algorithm/
Line Segment Intersection Algorithm
November 11th I’ll be participating in the Southern California Regional ACM programing competition. This is my second time competing as well as Adam’s. One of our practice problems involved finding if a wall blocks the path between two points. At the t
bryceboe.com
Geometry Concepts part 2: Line Intersection and its Applications
…Read Section 1 Line-Line Intersection Finding a Circle From 3 Points Reflection Rotation Convex Hull In th
www.topcoder.com
'CS > Algorithms' 카테고리의 다른 글
| 에라토스테네스의 체를 활용한 소인수분해 (0) | 2024.02.23 |
|---|---|
| 브루트포스 알고리즘 (Brute force 알고리즘) (0) | 2023.03.15 |
| 벡터의 외적과 CCW (Counter ClockWise) (4) | 2022.11.15 |
| 누적 합(prefix sum), 2차원 누적합(prefix sum of matrix) with java (11) | 2022.08.09 |
| 분할 정복을 이용한 거듭제곱 최적화 (0) | 2022.04.05 |





댓글