문제 : boj18251

필요 알고리즘 개념
- 스위핑
- 문제를 단순화 시키면 사실 여러번의 스위핑을 통해 풀 수 있는 문제이다. 다만 이건 내 경우이고, 이 문제는 DP 등 다른 풀이들도 있다. 내가 푼 방식은 스위핑을 이용한 풀이이므로 그걸로 해설을 진행한다.
- bfs (너비 우선 탐색)
- 내 경우 트리의 루트부터 주어진 가중치들을 스위핑을 하기 위해 위치 순서대로 정렬하려고 bfs를 사용했다. 꼭 필요한 방식은 아니고, 이 역시 다양한 방식으로 가능하다. 혹시 bfs를 모른다면 이 글을 참고하자.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
제목부터 이미지까지 정말 킹받는 문제가 아닐 수 없다. 6번 틀린 후 정답 맞췄는데, 도저히 틀린채로 넘어갈 수 없었다..

1. 문제의 단순화
원래 축이 2개인 경우 혹시 축을 하나로 변경해도 풀 수 있지 않을지 생각해보면 은근히 가능한 경우가 많다. 그럼 일단 축이 하나뿐일 때는 풀 수 있을지 먼저 생각해보자. 아래처럼 축이 1개에 가중치가 있는 데이터가 있다.
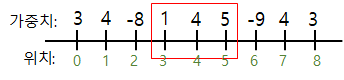
여기서 연속된 임의의 위치들을 골라 그 가중치 부분합이 최대가 되게 하고 싶다. 그렇다면 다음과 같은 규칙을 적용하면 될 것이다.
A. 위치 0에서 시작한다. 위치 0의 가중치합은 3이다.
B. 이제 위치를 하나씩 증가시키면서 가중치합을 구한다(i를 증가시키며, sum+=arr[i]). 가중치 합을 sum이라 하겠다.
C. sum이 음수가 되는 경우라면 sum을 0으로 초기화한다.
D. sum이 양수인 동안 계속해서 위치를 증가시키며 합을 구한다. 그러면서 존재했던 sum 중 최대값이 답이다.
그럼 위에서 제시된 데이터에 대해 다음과 같을 것이다. i는 위치 번호이다. sum은 현재까지의 가중치합이다.
i = 0 : sum = 3
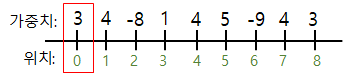
i = 1 : sum = 7

i = 2 : sum = -1
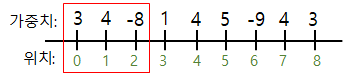
i = 3 : 이전 sum이 -1이므로 이전 구간은 필요가 없다. sum = 0부터 새로 시작한다. sum = 1

i = 4 : sum = 5
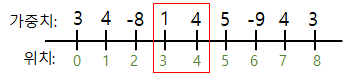
i = 5 : sum = 10
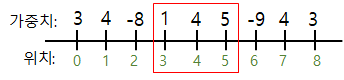
i = 6 : sum = 1. 현재 가장 큰 음수인 -9가 나왔지만 어쨌든 sum은 양수이므로 포함해서 진행해야한다.

i = 7 : sum = 5
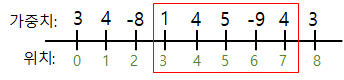
i = 8 : sum = 8

존재했던 sum 중 가장 큰 값은 10이므로, 최대 가중치 합은 10이 된다. 위와 같이 1개 축에 대해서는 스위핑을 통해 답을 어렵지 않게 찾을 수 있다.
2. 원래 문제에 적용
이제 다시 원래 문제에 '1'을 적용할 수 있을지 생각해보자. 잘 생각해보면, 문제에서 제시된 포화이진트리의 각 지점을 (x,y)라 할 때, y값은 동일한 경우가 있지만, x값은 모두 다르다. 즉, 이전에 단순화 시킨 문제로 이 문제를 변경할 수 있다!! 그럼 입력에서 주어진 포화이진트리만 좌측부터 순서대로 x값을 알 수 있다면 스위핑을 통해 답을 구할 수 있을 것이다..?
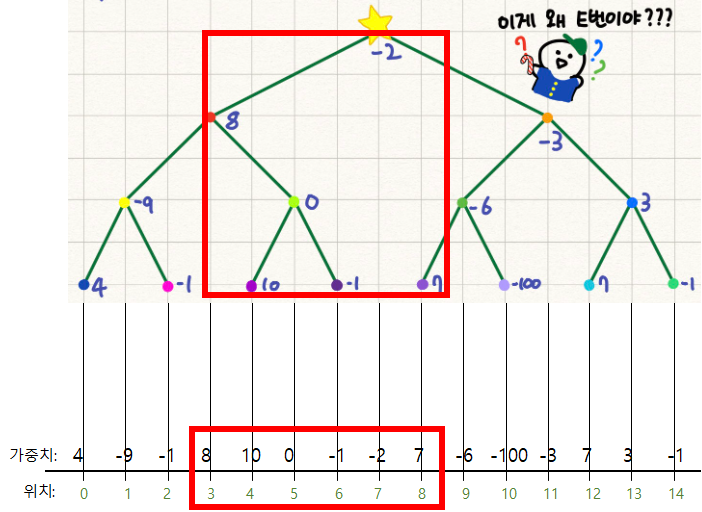
근데 사실 이것만 가지곤 안된다. 이런 경우는 어떨까? 위 처럼 직사각형을 배치할 경우, 1축으론 범위가 3개로 나뉘어졌다. 이럼 스위핑을 적용시킬 수 없다 ㅠ.

그럼 어떻게 하냐면, y값을 기준으로 모든 서로다른 y 값들에 존재하는 x값들을 별도로 생각해보는거다. 그림을 보면 이해 가능할 것이다. 이하 문제에서 제시된 예시에 대해 모든 서로다른 y쌍의 구간을 나타냈다.
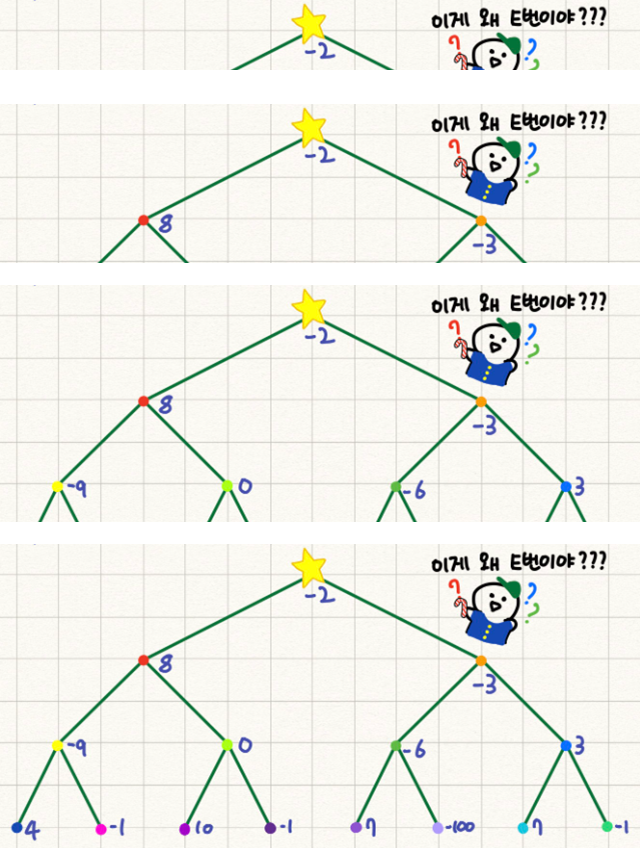
---

---

---

이 때 1개축으로 나타낸 데이터는, 만약 서로 다른 y축값들에 포함되는 데이터가 구분되어 있다면 매번 추가하거나 빼줄 수 있다. 코드에서는 아래처럼 진행했다. i가 낮은 y값, j가 높은 y값이라 할 때 i부터 j까지 해당 깊이의 x축 인덱스가 depthList에 포함되어 있다. 매번 i와 j (서로 다른 y의 구간 [i, j])를 위처럼 변경해주면서 스위핑 진행할 리스트를 조정하는 방식이다.
for (int s = i; s <= j; s++) {
ArrayList<Integer> depthList = depth[s];
for (int t = 0; t < depthList.size(); t++) {
hs.add(depthList.get(t));
}
}
그런데 이렇게 하는게 시간복잡도 상으로 가능할까? 우선 포화이진트리에 최대 깊이가 얼마나 되는지 먼저 생각해보면, log2(N)이 된다(밑이 2인 로그). N은 최대 262,143이므로 최대 깊이는 18이 될 것이다. 즉 y값은 최대 18가지의 서로 다른 값이 존재할 것이다. 그럼 y값에 대해 모든 구간 쌍을 확인할 경우 O(18^2)이면 된다. 그리고 스위핑 부분의 시간 복잡도는 O(N)이 될것이므로, O(N*(log2(N))^2) 이면 모든 y 구간에 대해 스위핑을 통해 답을 구해볼 수 있게 된다. N은 최대 262,143이므로, 최대 약 O(84,934,332)으로 통과가 가능하다(대략 O(1억)을 1초로 잡고 풀면 얼추 맞다.).
문제에서는 루트부터 가중치가 주어진다. 따라서 내 경우엔 BFS를 통해 각 깊이별 리스트를 만들었다. 코드로는 다음과 같다. x값 계산이 중요하다. 문제에서 제시된 대로 정할 경우 겹치지 않게 만들 수 있다. k는 log2(N)이다. 주석을 참고해보자.
Queue<int[]> q = new ArrayDeque<>();
q.add(new int[]{0, n/2});
StringTokenizer st = new StringTokenizer(br.readLine());
while (!q.isEmpty()) {
int[] cur = q.poll(); // cur[0]은 트리깊이, cur[1]은 x축 번호를 나타낸다.
depth[cur[0]].add(cur[1]);
arr[cur[1]] = Integer.parseInt(st.nextToken());
if (cur[0] == k-1) continue;
// (N+1)/2가 루트의 x값이고, 루트부터 좌우로 매번 +- 2^(k-2-깊이) 가 자식노드의 x값이다.
q.add(new int[]{cur[0]+1, cur[1]-(1<<(k-2-cur[0]))});
q.add(new int[]{cur[0]+1, cur[1]+(1<<(k-2-cur[0]))});
}
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
private int getK(int n) {
int k = 1;
while ((n/=2)!=1) {
k++;
}
return k;
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 1<<17);
int n = Integer.parseInt(br.readLine()) + 1;
int k = getK(n);
int[] arr = new int[n];
ArrayList<Integer>[] depth = new ArrayList[k];
for (int i = 0; i < k; i++) depth[i] = new ArrayList<>(1<<i);
Queue<int[]> q = new ArrayDeque<>();
q.add(new int[]{0, n/2});
StringTokenizer st = new StringTokenizer(br.readLine());
while (!q.isEmpty()) {
int[] cur = q.poll();
depth[cur[0]].add(cur[1]);
arr[cur[1]] = Integer.parseInt(st.nextToken());
if (cur[0] == k-1) continue;
q.add(new int[]{cur[0]+1, cur[1]-(1<<(k-2-cur[0]))});
q.add(new int[]{cur[0]+1, cur[1]+(1<<(k-2-cur[0]))});
}
long answer = Long.MIN_VALUE;
for (int i = 0; i < k; i++) {
for (int j = i; j < k; j++) {
HashSet<Integer> hs = new HashSet<>();
for (int s = i; s <= j; s++) {
ArrayList<Integer> depthList = depth[s];
for (int t = 0; t < depthList.size(); t++) {
hs.add(depthList.get(t));
}
}
long sum = 0;
for (int x = 1; x < n; x++) {
if (!hs.contains(x)) continue;
sum+=arr[x];
if (sum > answer) answer = sum;
if (sum < 0) {
sum = 0;
continue;
}
}
}
}
System.out.println(answer);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 5993 - Invasion of the Milkweed (java) (0) | 2022.09.08 |
|---|---|
| [자바] 백준 15489 - 파스칼 삼각형 (java) (2) | 2022.09.07 |
| [자바] 백준 24498 - blobnom (java) (0) | 2022.09.06 |
| [자바, C++] 백준 2118 - 두 개의 탑 (java cpp) (2) | 2022.09.06 |
| [자바] 백준 1174 - 줄어드는 수 (java) (0) | 2022.09.05 |





댓글