문제 : boj15352
1. 우선 '행동 2'만 존재할 경우 어떻게 풀 수 있을지 확인해보자.
입력으로 주어진 N개의 A값들에 대해 좌우로 인접한 항목이 같은 팬클럽 번호라면 그룹을 지어보자. 이 때, union-find를 사용하고 부모가 되는 노드에 차수를 입력해둔다고 한다면 '행동 2'에 대해 O(1)로 부모의 차수를 출력하는 것 만으로 결과를 낼 수 있다.
예를들어 parents[a]에 대해 parents[a] >= 0일 경우 부모의 번호, parents[a] < 0일 경우 부모 중 하나이며, 그 부모에 그룹지어져 있는 노드의 개수라고 하면 예제 입력 1은 다음과 같이 나타낼 수 있다.

union-find의 사용방법은 다양한 편이므로, 어쨌든 해당 그룹에 포함된 개수를 한방에 알 수만 있도록 짜면 된다. 위와 같이 표현할 경우 만약 쿼리가 '2 2'와 같이 들어온다면, find()를 통해 바로 해당 그룹의 부모인 parents[1]의 값에 x-1을 한 값을 출력하면 된다.
정리하자면, 만약 '행동 2'만 존재하는 문제였다면 union-find에 해당 그룹의 차수를 표현할 수 있도록 짜기만 한다면, 처음에 입력받을 때 인접한 항목에 대해 union만 해두면 이후 q개의 쿼리에 대해 각각 O(1)로 바로바로 찾을 수 있다.
2. '행동 1'을 처리해보자. 우선은 삭제 O(logN), 좌우 탐색 O(logN) 방식!
이제 '행동 1'을 처리해보자. 예를들어 A들이 '1 1 3 1 1' 이런식이었다고 해보자. 그럼 좌측 팬클럽1이 그룹지어져 있고, 우측 팬클럽1도 그룹지어져 있을 것이다. 이 때 중앙의 팬클럽3이 '행동 1'을 통해 삭제된다면 어떻게 해야할까? 떨어져 있던 좌측 그룹과, 우측 그룹도 동일하게 팬클럽1 이므로 합쳐지면 된다. 즉 union을 해줘야 한다.
따라서 '행동 1'이 발생할 경우 우선 해당 팬을 삭제한다. 그 후 삭제하면서 그 좌측과 우측에 남아있는 팬의 팬클럽 번호를 확인해 동일하다면 그룹지어주면 된다. 그럼 특정 번호를 빠르게 삭제할 수 있고, 빠르게 그 좌측과 우측에 남아 있던 팬의 번호를 알 수 있는 방법을 취하면 된다.
우선 처음에 내 경우엔 TreeSet(정확힌 Red-Black Tree로 구현되어 있음)을 활용해 이분탐색으로 생각해봤다. 이 경우 '행동 1'에 대해 대략 O(logN), 존재하는 값 중 삭제한 값보다 작은 값 탐색에 O(logN), 큰 값 탐색도 마찬가지로 O(logN)이 필요할 것이다. 이 때, 어차피 '행동 2에 대해 퇴출된 사람은 대상이 되지 않습니다.' 라는 조건에 따라 해당 팬 번호는 등장하지 않을 것이므로 삭제되었다고 해서 parents 배열에 뭔가 처리를 해줄 필요는 없다. 굳이 부모를 바꾸려 하지 않아도 된다. 그냥 해당 그룹에서 하나가 빠진 것이므로, 해당 그룹 부모의 차수를 하나 줄여주면 된다(내 경우엔 음수로 차수를 표기했으므로 +1을 해준다.)
이 경우 전체적인 로직 순서는 다음과 같다.
2.1 '행동 1'이 들어올 경우('1 b'의 형태의 쿼리) TreeSet에서 b를 삭제하고, b가 속한 그룹의 차수를 조절한다. 그리고 그보다 낮은 팬과 높은 팬 번호를 이분탐색으로 찾는다(TreeSet에서는 lower, higher. c++에서의 lower_bound와 upper_bound와 비슷하다.). 그 두 팬의 팬클럽 번호가 같다면 union을 해준다.
2.2 '행동 2'가 들어올 경우('2 b'의 형태), 단순히 parents[find(b)]를 통해 바로바로 선물을 준 팬의 수를 확인 가능하다.
'2'의 과정을 통해 짠 코드는 아래와 같다. (※ '3'에서 더 빠른 방법에 대해 다룬다.)
...
public class Main {
TreeSet<Integer> remain;
private int[] parents, arr;
private int find(int a) {
if (parents[a] < 0) return a;
return parents[a] = find(parents[a]);
}
private void union(int a, int b) {
a = find(a);
b = find(b);
if (a == b) return;
int h = parents[a]<parents[b]?a:b;
int l = parents[a]<parents[b]?b:a;
parents[h] += parents[l];
parents[l] = h;
}
private void init(int n) {
remain = new TreeSet<>();
for (int i = 1; i <= n; i++) remain.add(i);
parents = new int[n+1];
Arrays.fill(parents, -1);
arr = new int[n+1];
}
private void solution() throws Exception {
int k = nextInt();
int n = nextInt();
init(n);
arr[1] = nextInt();
for (int i = 2; i <= n; i++) {
arr[i] = nextInt();
if (arr[i] == arr[i-1])
union(i-1, i);
}
int q = nextInt();
long sum = 0;
while (q-->0) {
int a = nextInt();
int b = nextInt();
if (a == 2) {
sum-=parents[find(b)];
} else {
remain.remove(b);
parents[find(b)]++;
Integer lower = remain.lower(b);
Integer higher = remain.higher(b);
if (lower != null && higher != null && arr[lower] == arr[higher])
union(lower, higher);
}
}
System.out.println(sum);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}
...
3. 이번엔 '행동 1'을 삭제 O(1), 좌우 탐색 O(1) 정도로 해보자.
'2'의 방식에서 이분탐색보다 더 빠르게 할 방법이 있다! 참고로 백준 기준 시간차이는 '2'가 2300ms, '3'이 500ms 였다.
n개의 배열을 2개 더 추가해서 하나는 자신의 왼쪽 팬 번호, 나머지 하나는 자신의 오른쪽 팬 번호를 기입해보자. left와 right라고 하겠다. n=5인 경우에 대해 그럼 맨 처음엔 아래와 같이 표현할 수 있을 것이다.
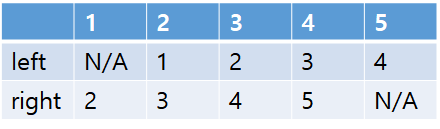
이 때 만약 '3'이 삭제되면 어떻게 변경되면 다음과 같이 될 것이다. 즉 right[left[3]] = right[3]이 될 것이고, left[right[3]] = left[3]이 될 것이다(3의 우측에 있던 녀석이 3의 좌측에 있던 녀석의 오른쪽에 붙게 될 것이고, 3의 좌측에 있던 녀석이 3의 우측에 있던 녀석의 왼쪽에 붙게 될 것임).

마찬가지로 이 상태로 차례대로 2,4를 더 지워보겠다.

이런식으로 한다면 '2'의 과정보다 훨씬 빠르게, O(1)로 삭제연산이 가능하며, 심지어 자신의 좌측에 있는 삭제되지 않은 값 중 가장 큰 값과, 자신의 우측에 있는 삭제되지 않은 값 중 가장 작은 값또한 O(1)로 알 수 있다. 그럼 여기에 '1'의 과정만 더해주면 된다.
전체 로직 순서는 다음과 같다.
3.1 '행동 1'이 들어올 경우('1 b'의 형태), left[b]와 right[b]의 팬클럽 번호가 동일하다면 union해준다. 그 후 right[left[b]] = right[b], left[right[b]] = left[b]를 해준다.
3.2 '행동 2'가 들어올 경우('2 b'의 형태), 단순히 parents[find(b)]를 통해 바로바로 선물을 준 팬의 수를 확인 가능하다.
코드 : github
import java.io.DataInputStream;
import java.util.Arrays;
public class Main extends FastInput {
private static final int OUT_BOUND = -1;
private int[] parents, arr, left, right;
private int find(int a) {
if (parents[a] < 0) return a;
return parents[a] = find(parents[a]);
}
private void union(int a, int b) {
a = find(a);
b = find(b);
if (a == b) return;
int h = parents[a]<parents[b]?a:b;
int l = parents[a]<parents[b]?b:a;
parents[h] += parents[l];
parents[l] = h;
}
private void init(int n) {
parents = new int[n+1];
Arrays.fill(parents, -1);
arr = new int[n+1];
left = new int[n+1];
right = new int[n+1];
}
private void solution() throws Exception {
nextInt(); //throw
int n = nextInt();
init(n);
for (int i = 1; i <= n; i++) {
arr[i] = nextInt();
if (arr[i] == arr[i-1])
union(i-1, i);
left[i] = i-1;
right[i] = i+1;
}
left[1] = right[n] = OUT_BOUND;
long sum = 0;
int q = nextInt();
while (q-->0) {
int a = nextInt();
int b = nextInt();
if (a == 2) {
sum-=parents[find(b)];
} else {
parents[find(b)]++;
int lower = left[b];
int higher = right[b];
if (lower != OUT_BOUND && higher != OUT_BOUND && arr[lower] == arr[higher])
union(lower, higher);
if (lower != OUT_BOUND)
right[lower] = higher;
if (higher != OUT_BOUND)
left[higher] = lower;
}
}
System.out.println(sum);
}
public static void main(String[] args) throws Exception {
initFI();
new Main().solution();
}
}
class FastInput {
private static final int DEFAULT_BUFFER_SIZE = 1 << 16;
private static DataInputStream inputStream;
private static byte[] buffer;
private static int curIdx, maxIdx;
protected static void initFI() {
inputStream = new DataInputStream(System.in);
buffer = new byte[DEFAULT_BUFFER_SIZE];
curIdx = maxIdx = 0;
}
protected static int nextInt() throws Exception {
int ret = 0;
byte c = read();
while (c <= ' ') c = read();
do {
ret = ret * 10 + c - '0';
} while ((c = read()) >= '0' && c <= '9');
return ret;
}
private static byte read() throws Exception {
if (curIdx == maxIdx) {
maxIdx = inputStream.read(buffer, curIdx = 0, DEFAULT_BUFFER_SIZE);
if (maxIdx == -1) buffer[0] = -1;
}
return buffer[curIdx++];
}
}'PS > BOJ' 카테고리의 다른 글
| 백준 1287 자바, 파이썬 - 할 수 있다 (BOJ 1287 JAVA, Python) (0) | 2022.02.05 |
|---|---|
| 백준 23258 자바 - 밤편지 (BOJ 23258 JAVA) (0) | 2022.02.04 |
| 백준 2688 자바 - 줄어들지 않아 (BOJ 2688 JAVA) (0) | 2022.02.03 |
| 백준 15992 자바 - 1, 2, 3 더하기 7 (BOJ 15992 JAVA) (0) | 2022.02.02 |
| 백준 20126 자바 - 교수님의 기말고사 (BOJ 20126 JAVA) (0) | 2022.02.01 |





댓글