문제 : boj23258
개인적으로 오늘 푼 플3 문제보다 몇배는 어려웠다. 심지어 플로이드 와샬 알고리즘을 정확히 이해해야 풀 수 있는 문제라고 추천을 받고 풀게되어서 일단 플로이드 와샬을 써야 한다는 점은 알고 풀게 되었는데 그런데도 엄청 해맸다 ㅠ
아무튼 플로이드 와샬을 써보려면 이 문제는 꼭 풀어봐야 할 것 같다. 플로이드 와샬을 이해하는데 도움이 되는 매우 좋은 문제라 생각한다.
1. '2^C 방울 이상 마시면 안된다'의 의미
우선 이 부분부터가 문제였다. 처음엔 뭔가 장난스럽게, 좀 더 복잡하게 보일려고 이렇게 작성했다고 생각했다. 그래서 2^X, 2^C에서 '2^' 부분은 때고 X, C로만 생각했는데 당연히 제대로 답이 안나왔다. 결론적으로 키 아이디어에 해당하는 부분으로 사실 C<=N+1 이라는 입력 제한에서 힌트를 얻었다 ㅋㅋ. 결국 [ 2^C방울 '이상'을 마시면 안된다 == C-1번 이하의 집만 지나서 도달할 수 있어야 한다. ] 라는 뜻이다. 왜냐하면 공대생이라면 2진법에서 많이 봤듯이 2^1 + 2^2 + ... 2^(C-1) < 2^C 이기 때문이다.
2. 우선 '1'을 제외하고 생각해보자.
이 경우 총 500000개의 쿼리를 처리해야 하고, s->e로 가는 최단거리만 출력하면 될 것이다. 그리고 N이 총 300개밖에 안되므로 O(N^3)이 걸리는 플로이드 와샬로 모든 최단거리를 미리 구해두고 각 쿼리에 대해 바로바로 출력하는 방식을 쉽게 생각해볼 수 있다.
3. 이제 '1'의 내용을 플로이드 와샬에 접목시켜보자.
결론적으로 플로이드 와샬을 진행하면서 X이하만을 지나오는 부분에 대해 DP도 진행해야 한다. 일반적인 플로이드 와샬이라면 arr[a][b]와 같은 2차월 배열 하나로 a에서 b로 가는 최단거리를 알 수 있다. 이 문제에서는 x 이하의 경유지만 경유해서 이동한 경우의 최단거리를 알 수 있도록 arr[a][b][x] 와 같이 3차원 배열로 진행했다. arr[a][b][x]는 'x 이하의 경유지만을 경유해서 a에서 b로 가는 최단거리' 이다.
그럼 이걸 어떻게 구할 수 있을지 생각해봐야 하는데, 우선 다음의 일반적인 경우의 플로이드 와샬 코드를 봐보자. 3중 반복문을 사용해서 우선 가장 바깥쪽의 k가 경유지를 의미하고, i와 j는 i에서 j로 가는 경우를 뜻한다. 그럼 결국 i->j와 i->k + k->i 중 작은 것을 택하는 방식이다. 즉, 바로 가는 것과 k를 경유해서 가는 것 중 빠른 길을 택하는 방식이다.
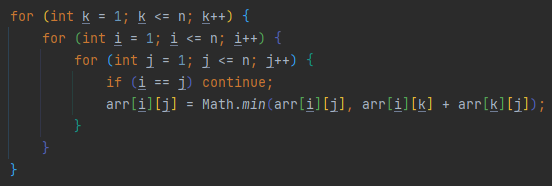
그럼 이번엔 이 문제에 맞게 arr[a][b][k]로 선언해서 진행한 코드를 봐보자. 결국 이 경우는 k를 경유해서 i에서 j로 간 경우에 대해 중간과정을 모두 저장한 셈이다. 그리고, k는 1부터 n까지 증가하므로 결국 arr[a][b][k]는 'k 이하의 경유지만을 거쳐서 진행한'게 된다. 그리고 이 문제에서는 '출발지와 도착지를 제외하고 이동하는 동안' 이라고 했으므로 이렇게 dp를 진행해두면 각 쿼리에서 입력으로 들어온 C, s, e에 대해 단순히 arr[s][e][C-1]의 값만 출력해주면 된다.

이 부분은 나만 헷갈렸을 수도 있는데, s == e 인 경우 -1이 아니라 0을 출력해줘야 한다. 지금 보니 당연한 것 같은데 이것때문에 맞왜틀을 꽤 외쳤다ㅋㅋ.
코드 : github
import java.io.DataInputStream;
import java.io.IOException;
public class Main extends FastInput {
private static final int INF = 170324*300+1;
private void init(int n, int[][][] arr) {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (i == j || i == k || k == j)
arr[i][j][k] = arr[i][j][k-1];
else
arr[i][j][k] = Math.min(arr[i][j][k-1], arr[i][k][k-1] + arr[k][j][k-1]);
}
}
}
}
private void solution() throws Exception {
int n = nextInt();
int q = nextInt();
int[][][] arr = new int[n+1][n+1][n+1];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
arr[i][j][0] = nextInt();
if (arr[i][j][0] == 0)
arr[i][j][0] = INF;
}
}
init(n, arr);
StringBuilder sb = new StringBuilder();
while (q-->0) {
int c = nextInt();
int s = nextInt();
int e = nextInt();
sb.append(s==e?0 : (arr[s][e][c-1] == INF ? -1 : arr[s][e][c-1])).append('\n');
}
System.out.print(sb);
}
public static void main(String[] args) throws Exception {
initFI();
new Main().solution();
}
}
class FastInput {
private static final int DEFAULT_BUFFER_SIZE = 1 << 16;
private static DataInputStream inputStream;
private static byte[] buffer;
private static int curIdx, maxIdx;
protected static void initFI() {
inputStream = new DataInputStream(System.in);
buffer = new byte[DEFAULT_BUFFER_SIZE];
curIdx = maxIdx = 0;
}
protected static int nextInt() throws IOException {
int ret = 0;
byte c = read();
while (c <= ' ') c = read();
do {
ret = ret * 10 + c - '0';
} while ((c = read()) >= '0' && c <= '9');
return ret;
}
private static byte read() throws IOException {
if (curIdx == maxIdx) {
maxIdx = inputStream.read(buffer, curIdx = 0, DEFAULT_BUFFER_SIZE);
if (maxIdx == -1) buffer[0] = -1;
}
return buffer[curIdx++];
}
}'PS > BOJ' 카테고리의 다른 글
| 백준 1590 자바 - 캠프가는 영식 (BOJ 1590 JAVA) (0) | 2022.02.06 |
|---|---|
| 백준 1287 자바, 파이썬 - 할 수 있다 (BOJ 1287 JAVA, Python) (0) | 2022.02.05 |
| 백준 15352 자바 - 욱제와 그의 팬들 (BOJ 15352 JAVA) (0) | 2022.02.04 |
| 백준 2688 자바 - 줄어들지 않아 (BOJ 2688 JAVA) (0) | 2022.02.03 |
| 백준 15992 자바 - 1, 2, 3 더하기 7 (BOJ 15992 JAVA) (0) | 2022.02.02 |





댓글