문제 : boj15992
1. 단순화 해서 생각해보기
우선 '사용한 수의 개수는 m개' 라는 조건이 없다고 생각해보자. 이 경우 1부터 n까지의 1차원 DP로 풀 수 있다. dp[a]를 a를 1,2,3을 더해서 표현할 수 있는 가지수라고 할 경우, 점화식은 다음과 같을 것이다. 즉, a를 1부터 n까지 증가시키며 다음의 점화식을 적용한 DP를 진행하면 된다.
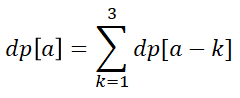
2. 사용한 수의 개수가 m개
'1'에서 조건이 하나 더 추가되었다. 그러니 2차원 DP로 확장시키면 된다. dp[a][b]를 a를 1,2,3을 b번 더해서 표현할 수 있는 가지수라고 할 경우, 점화식은 다음과 같을 것이다. 마찬가지로 a는 1부터 n까지 증가시키면 되고, 이 때 b는 1부터 min(a, m) 까지 증가시키면서 구하면 된다(그냥 b도 1부터 m까지 증가시켜도 된다. 그냥 약간의 백트래킹을 넣어 시간복잡도를 줄이기 위해서이다. 어차피 최소로 더해지는 값이 1이므로 a를 표현할 때 a번 초과로 더해지는 경우는 없다.).

3. 약간의 주의점
3.1 각 TC에 대해 n, m을 받아 dp = new int[n][m]; 를 하는 것 보다, 그냥 처음에 n=1000, m=1000인 경우에 대해 한번만 dp를 진행하고, 이후로는 TC의 n, m을 입력받아 바로바로 dp[n][m]을 출력하기만 하는 것이 훨씬 효율적이다. (시간복잡도가 O(tnm) -> O(nm+t) 로 줄어듬)
3.2 1,000,000,009로 나누는걸 잊으면 안된다. 덧셈에 대해서 나머지 연산도 분배법칙( 즉, (a+b)%c == (a%c + b%c)%c )이 성립하므로 매번 나머지 연산을 진행하면 int형 범위를 넘어갈 일도 없으므로 편하게 진행할 수 있다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private static final int MOD = 1000000009;
private int[][] dp;
private int proc(int n, int m) {
dp = new int[n+1][m+1];
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
if (j > m) break;
for (int k = 1; k <= 3; k++) {
if (i-k < 0) break;
dp[i][j] += dp[i-k][j-1];
dp[i][j] %= MOD;
}
}
}
return dp[n][m];
}
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
proc(1000, 1000);
while (t-->0) {
StringTokenizer st = new StringTokenizer(br.readLine());
int answer = dp[Integer.parseInt(st.nextToken())][Integer.parseInt(st.nextToken())];
sb.append(answer).append('\n');
}
System.out.print(sb);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| 백준 15352 자바 - 욱제와 그의 팬들 (BOJ 15352 JAVA) (0) | 2022.02.04 |
|---|---|
| 백준 2688 자바 - 줄어들지 않아 (BOJ 2688 JAVA) (0) | 2022.02.03 |
| 백준 20126 자바 - 교수님의 기말고사 (BOJ 20126 JAVA) (0) | 2022.02.01 |
| 백준 1439 자바 - 뒤집기 (BOJ 1439 JAVA) (0) | 2022.01.31 |
| 백준 18242 자바 - 네모네모 시력검사 (BOJ 18242 JAVA) (0) | 2022.01.30 |





댓글