문제 : boj2133
1.
우선, 2x1과 1x2짜리 타일을 사용해야 하므로 무슨짓을 하던 n이 홀수라면 전체 칸 수(3 x n)가 홀수이므로 2칸짜리 타일로 타일링이 불가능하다. 즉, n이 짝수일 때만 타일링이 가능하다. 이 부분은 예외로 처리해준다.
2.
가장 기본적인 규칙성을 찾아보자. n=2일 때 3가지 모양이 나온다.

3.
그럼 n=4일 때는 n=2일 때 나왔던 모양에서 각각의 경우 3가지 모양이 더 추가되므로 'n=2일때의 모양 x 3'이 됨을 쉽게 알 수 있다. 예를 들어 위 n=2일때 중 첫번째 그림에 대해서만 그려보면 다음과 같다.
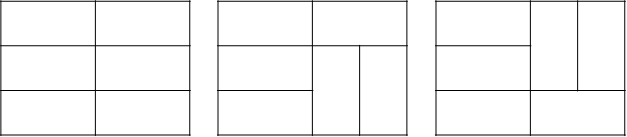
일단 여기까지, f(n)을 3 x n 타일링에서 n개의 가로칸으로 가능한 타일링의 경우의 수라 하자. 그럼 f(4) = f(2) * 3 임을 알 수 있다.
4.
다음으로 n=4일 때, 예외로 추가되는 규칙성을 확인해보자. 2개씩 나눴을 때 중간에 겹치는 부분을 활용한 다음의 타일링이 있다.

그럼 일단 n=4일 때, f(4) = f(2) * 3 + 2 = 11 임을 알 수 있다.
혹시 다른 규칙성은 없는지 파악하기 위해 n=6으로 넘어가자.
5.
n=6일 때, 일단 f(6) = f(4) * 3 임은 확실하다(4칸으로 가능한 모든 타일링 경우에 2칸으로 가능한 타일링 3가지를 매칭 가능하므로). 그럼 f(6)에서 가능한 예외를 찾아보자. 우선 n=4의 예외의 경우에서 확장한 n=6의 예외이다.
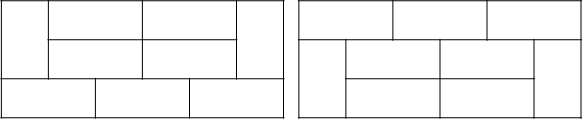
위의 예외 부분은 마찬가지 방식으로 확장되어 n=8, n=10, ... 에도 존재한다.(위의 예외와 확장된 예외들은 세로선을 나눌 수 없으므로 f(n)에 대해 고유한 예외이다. 고유한 예외 이외의 예외는 '6'에서 살펴볼 수 있다.)
따라서 f(n) = f(n-2) * 3 + 2 까지는 항상 확정시킬 수 있다. 여기서 좀 더 생각해볼게 있다.
6.
n=2일 때 예외는 0개였고, n=4 부터는 항상 2개였다. 그럼 칸이 늘어나면서 n=6일 때, 좌측 2칸을 제외하고 우측 4칸에서도 n=4일 때의 예외를 적용시킬 수 있다. 즉, 다음과 같은 경우이다. 위 '4'의 n=4일 때의 예외가 우측에 붙은 형태이다.

따라서 f(6) = f(4) * 3 + 2 + f(2) * 2 가 됨을 알 수 있다.
그럼 n=8일 땐, 동일한 발상에 따라 f(8) = f(6) * 3 + 2 + f(2)*2 + f(4)*2 가 됨을 알 수 있다.
(f(2)*2는 n=2일 때의 경우에 n=6일 때의 예외 2가지를 우측에 배치한 경우, f(4)*2는 n=4일 때의 경우에 n=4일 때의 예외 2가지를 우측에 배치한 경우)
그럼 최종적으로 점화식은 다음과 같다.

이제 DP로 위 점화식을 계산하면 된다.
작성한 코드의 경우 어차피 홀수부분은 제외되므로 배열 메모리를 아끼기 위해 n을 2로 나누어 계산했지만, 결국 위 공식과 동일한 동작을 하는 코드이다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.function.Function;
public class Main {
Function<Integer, Boolean> isOdd = (n) -> (n&1)==1;
public void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
if (isOdd.apply(n)) {
System.out.println(0);
return;
}
int[] dp = new int[Math.max(n/2, 2)];
dp[0] = 3;
dp[1] = 11;
int tmp = 0;
for (int i = 2; i < n/2; i++) {
dp[i] = dp[i-1] * 3 + 2 + (tmp+=dp[i-2]*2);
}
System.out.println(dp[n/2-1]);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}
'PS > BOJ' 카테고리의 다른 글
| 백준 2491 자바 - 수열 (BOJ 2491 JAVA) (0) | 2021.12.31 |
|---|---|
| 백준 2225 자바 - 합분해 (BOJ 2225 JAVA) (0) | 2021.12.30 |
| 백준 2193 자바 - 이친수 (BOJ 2193 JAVA) (0) | 2021.12.30 |
| 백준 2294 자바 - 동전 2 (BOJ 2294 JAVA) (0) | 2021.12.30 |
| 백준 2293 자바 - 동전 1 (BOJ 2293 JAVA) (0) | 2021.12.29 |





댓글