문제 : boj2225
1.
0부터 N까지에서 '0부터' 부분 때문에 좀 헷갈렸다. '덧셈의 순서가 바뀐 경우는 다른 경우로 센다' 라는 부분 때문에, 예를들어서 N이 1이라 해도 K가 5라면 1+0+0+0+0 / 0+1+0+0+0 / ... / 0+0+0+0+1 이 가능해진다 ㅋㅋㅋ
0의 더하는 순서라니 인지적으로는 좀 이상하긴 하지만, 사실 문제 푸는데는 상관없다! '2'를 보면 알겠지만, 그냥 1부터 N까지라고 해도 점화식이 달라질 뿐이다.
2.
K-1개의 수를 합해 만든 어떠한 값이 있다. 이 값에 0부터 N까지의 정수를 더한다면 K-1개의 수로 만든 합에 1개의 정수를 더 더한 것이므로, K개의 수를 사용해 만든 어떠한 합이 될 것이다.
그렇다면 0부터 N까지의 정수를 사용해서, X개의 수를 합해 더한 값이 Y가 되려면 어떻게 해야 할까?-> X-1개의 수의 합이 Y인 값에 0을 더한다.-> X-1개의 수의 합이 Y-1인 값에 1을 더한다.-> X-1개의 수의 합이 Y-2인 값에 2를 더한다.....
-> X-1개의 수의 합이 Y-N인 값에 N을 더한다.
이걸 작은 경우부터 계속해나가면 K개를 더해 합이 N이 되는 경우를 찾을 수 있을 것이다.
3.
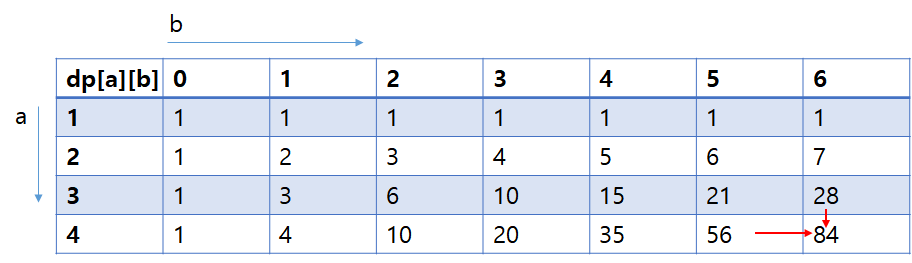
dp[a][b]를 a개의 수를 합해 b를 만드는 경우의 수라고 하자.(a<=k, b<=n) 그리고 '2'의 로직을 이 dp 배열에 적용해서 '예제 입력 2'인 '6 4'에 적용해보자.
우선 초기값들로 명백한 값을 작성해두자. 1개의 값(a=1인 행)만 사용해 b를 표현할 방법은 하나 뿐이다(순서대로 0부터 n까지의 값 하나만 사용).
다음으로 0을 표현할 경우의 수(b=1인 열)는 0, 0+0, 0+0+0, 0+0+0+0 이므로 각각 1가지 방법 뿐이다.

이제 각 행의 열들에 남은 값들을 채워보자. '2'를 이 dp[a][b]에 적용한 점화식은 다음과 같다.

표에서 위 점화식이 적용되는 범위를 보면, 예를들어 dp[2][5]를 구하는건 다음과 같이 하면 된다.

마찬가지로 나머지 값도 채워보자. 이하는 모두 채운 경우이다. '예제 입력2'의 답인 84가 구해짐을 볼 수 있다.

4.
그런데 이러면 O(K x N^2)의 시간복잡도가 나온다. 크게 문제없는 복잡도긴 하지만, 좀 더 줄여볼 수 있다. 위의 점화식에서 시그마를 b까지 더하는 것에서, b-1까지만 더해보자. 그럼 dp[a-1][b]을 빼낼 수 있고, 뒤의 시그마 식은 dp[a][b-1]과 동일하다.

따라서, dp[a][b] = dp[a-1][b] + dp[a][b-1] 로 시그마를 없애고 간략하게 변경할 수 있다. 이 경우 시간복잡도 O(K x N)에 연산 가능하다.
표로 보자면 단순히 좌측과 위의 값만 더해나간 것이다.
5.
마지막으로 1,000,000,000 으로 나눈 나머지를 출력하는 부분에 대해서는, 나머지 연산(모듈러 연산)에 대해 덧셈에서 교환법칙이 성립함을 안다면( 즉, (x+y+z)%m == x%m + y%m + z%m ) 매번 dp[a][b]를 계산 후 나머지만 저장하고 있어도 최종 답을 구하는데 문제 없음을 알 수 있다.
이 때, int형은 최대 2^31-1 = 대략 21억까지 표현 가능하다. '4'의 점화식을 사용할 경우 10억으로 나눈 나머지값이 2개가 합쳐진다. 따라서 연산 과정에서 모든 수는 최대 20억-2 까지 존재할 수 있으므로, int 형으로 모든 연산 표현이 가능하다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
private static final int MOD = 1000000000;
public void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
int[][] dp = new int[k+1][n+1];
Arrays.fill(dp[1], 1);
for (int i = 1; i <= k; i++) dp[i][0] = 1;
for (int i = 2; i <= k; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
dp[i][j] %= MOD;
}
}
System.out.println(dp[k][n]);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}
'PS > BOJ' 카테고리의 다른 글
| 백준 10819 자바 - 차이를 최대로 (BOJ 10819 JAVA) (0) | 2022.01.01 |
|---|---|
| 백준 2491 자바 - 수열 (BOJ 2491 JAVA) (0) | 2021.12.31 |
| 백준 2133 자바 - 타일 채우기 (BOJ 2133 JAVA) (0) | 2021.12.30 |
| 백준 2193 자바 - 이친수 (BOJ 2193 JAVA) (0) | 2021.12.30 |
| 백준 2294 자바 - 동전 2 (BOJ 2294 JAVA) (0) | 2021.12.30 |





댓글