--- 이해하기 어렵게 작성한 것 같아서 새로 작성했습니다. 이 글(링크)을 보시는게 더 나을 것 같습니다. ---
문제 : boj10986
i번 까지 누적합을 계산한 값이 arr[i]라고 하자(1<=i<=N). 이 때 [a, b] 구간의 합은 arr[b]-arr[a-1]이 될 것 이다. 그리고 이 문제에서는 [a, b] 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구해야 한다.
그럼 이번엔 arr[a-1]을 M으로 나눈 나머지가 X라고 해보자. 그렇다면 특정 인덱스 값 b에 대해 arr[b]의 값을 M으로 나눈 값이 X인 곳이 있다면 arr[b]-arr[a-1]을 M으로 나눈 나머지는 0이 된다. 왜냐하면 나누기 연산에 이하의 분배법칙이 적용되기 때문이다. 즉, arr[b]를 M으로 나눈 나머지가 X이고, arr[a-1]을 M으로 나눈 나머지가 X라면 arr[b]-arr[a-1]을 M으로 나눈 나머지는 X-X가 되므로 0이 된다는 말이다.

참고로 이 때 누적합으로 계산하지 않고 각각의 Ai를 M으로 나눈 나머지는 의미가 없다. 왜냐면 이건 연속된 값이 아니라, 임의의 두 값에 대한 문제였을 때 의미가 있는 것이기 때문이다.
아무튼 그러니 각 Ai를 입력받으면서 누적합을 구한다. 이하 코드에서는 'sum'이 누적합 역할을 한다. 그리고 매번 누적합을 M으로 나눈 X를 구하고, 그 전까지 몇 번 나왔는지 세둔다. 이하 코드에서 cnt[]가 해당 역할을 한다. 매번 누적합을 M으로 나눈 값으로 유지해도 되는 이유는 나머지 연산에 이하의 분배법칙도 적용되기 때문이다. 즉, 어차피 M으로 나눈 값을 유지할 생각이라면 arr[b]%M == (arr[1]%M+arr[2]%M+arr[3]%M+...+arr[B]%M)%M 이므로 매번 나누어도 결과를 구하는데 상관이 없다(매번 안나눌꺼면 long을 써야한다.)
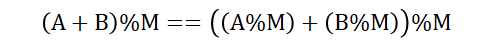
X를 구했다면, 이전에 X가 나온 횟수만큼 결과값(코드의 answer)에 더해주면 된다. 이 때 주의점은 현재까지의 합을 M으로 나눈 나머지가 0이라면 1부터 현재까지 그 자체도 M으로 나눈 나머지가 0인 것이므로 결과값에 1개를 더해줘야 한다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
private void solution() throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int sum = 0;
int[] cnt = new int[1000];
long answer = 0;
st = new StringTokenizer(br.readLine());
while (n-->0) {
int cur = Integer.parseInt(st.nextToken());
sum += cur;
sum %= m;
answer += cnt[sum];
cnt[sum]++;
if (sum==0) answer++;
}
System.out.println(answer);
}
public static void main(String[] args) throws Exception {
new Main().solution();
}
}'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 14725 - 개미굴 (boj java) (0) | 2022.06.08 |
|---|---|
| [자바] 백준 18818 - Iguana Instructions (boj java) (0) | 2022.06.08 |
| [자바] 백준 22938 - 백발백준하는 명사수 (boj java) (0) | 2022.06.06 |
| [자바] 백준 23808 - 골뱅이 찍기 - ㅂ (boj java) (0) | 2022.06.05 |
| [자바] 백준 24445 - 알고리즘 수업 - 너비 우선 탐색 2 (boj java) (0) | 2022.06.04 |





댓글