목차
문제 : boj17616

필요 알고리즘
- 그래프 이론, 그래프 탐색 (bfs, dfs)
- A와 B의 관계를 단방향 그래프로 볼 수 있는 직관이 필요한 문제이다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
우선 너비 우선 탐색(BFS)을 모른다면 '이 글'을 참고해보자.
문제로 주어진 부분을 그래프로 변경해 생각해보는 아이디어가 필요한 문제로, 교육적으로도 상당히 좋은 문제라 생각된다. 우선 'A가 학생 B보다 더 잘했다' 라는 데이터를 가지고 학생을 정점으로 하는 단방향 그래프를 만들어보자.
아래와 같은 데이터를 가지고 해보면
5 5 1
1 3
2 1
3 4
3 5
4 5
// 답은 2 2
이하처럼 나타낼 수 있다.
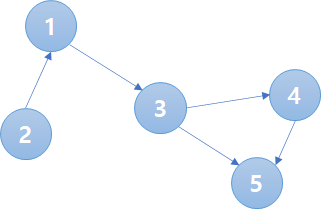
그럼 이게 뭘 나타낼 수 있을까? X=1 이므로 X부터 탐색해서 갈 수 있는 지점들의 수를 세보자. 이 경우 X를 제외하면 3개를 갈 수 있고, 간선을 등수가 높은쪽 -> 낮은쪽으로 그어둔 상태로 탐색을 했으므로 이건 즉 X=1 보다 더 등수가 낮음이 확실한 학생들의 수를 뜻한다. 즉, X 학생보다 등수가 낮은게 확실한 학생이 3명이므로 X는 1등일수도 있지만, 아무튼 확정된 가장 낮은 등수는 2등(=5-3) 이라고 할 수 있다. 1등도 가능하고 2등도 가능하지만, N명 중 자기보다 낮은 사람이 3명이 확정이므로 3,4,5등은 불가능하기 때문이다.

여기까지 이해했다면, 최대 등수도 구할 수 있을꺼다. 단방향 간선에서 X에서 도달 가능한 정점들이 있을때, 모든 간선의 방향을 반대로 바꿀 경우 그건 X로 도달 가능한 정점을 의미하게 된다. 자기보다 등수가 높음이 확정된 학생이 몇명인지 알면 되므로 반대로 간선을 B->A로 만들면 된다. 그리고 마찬가지로 X=1 부터 탐색을 진행하면 이번엔 X보다 등수가 높은 학생의 수를 알 수 있다. 말로 설명하자면, X번 학생보다 등수가 높음이 확정된 사람이 1명이므로 2,3,4,5등 일 수 있지만, 아무튼 최대치는 2등인 셈이다.

참고로 일단 그래프를 만들었다면 탐색은 bfs로 하던지 dfs로 하던지 어차피 도달 가능한 정점의 갯수만 알면 되므로 상관 없다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 1<<16);
public static void main(String[] args) throws Exception {
new Main().solution();
}
public void solution() throws Exception {
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int x = Integer.parseInt(st.nextToken());
List<Integer>[] bToA = new List[n+1];
List<Integer>[] aToB = new List[n+1];
for (int i = 1; i <= n; i++) {
bToA[i] = new ArrayList<>();
aToB[i] = new ArrayList<>();
}
while (m-->0) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
bToA[b].add(a);
aToB[a].add(b);
}
StringBuilder sb = new StringBuilder();
sb.append(bfs(n, x, bToA)).append(' ').append(n + 1 - bfs(n, x, aToB));
System.out.println(sb);
}
private int bfs(final int n, final int x, final List<Integer>[] edges) {
boolean[] v = new boolean[n+1];
Queue<Integer> q = new ArrayDeque<>();
q.add(x);
v[x] = true;
int cnt = 0;
while (!q.isEmpty()) {
int cur = q.poll();
cnt++;
for (int next : edges[cur]) {
if (v[next]) continue;
v[next] = true;
q.add(next);
}
}
return cnt;
}
}
'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 14257 - XOR 방정식 (java) (0) | 2023.08.11 |
|---|---|
| [자바] 백준 28251 - 나도리합 (java) (0) | 2023.08.11 |
| [자바] 백준 11912 - 격자 보존하기 (java) (0) | 2023.08.11 |
| [자바] 백준 2138 - 전구와 스위치 (java) (0) | 2023.08.11 |
| [자바] 백준 11066 - 파일 합치기 (java) (0) | 2023.08.10 |





댓글