목차
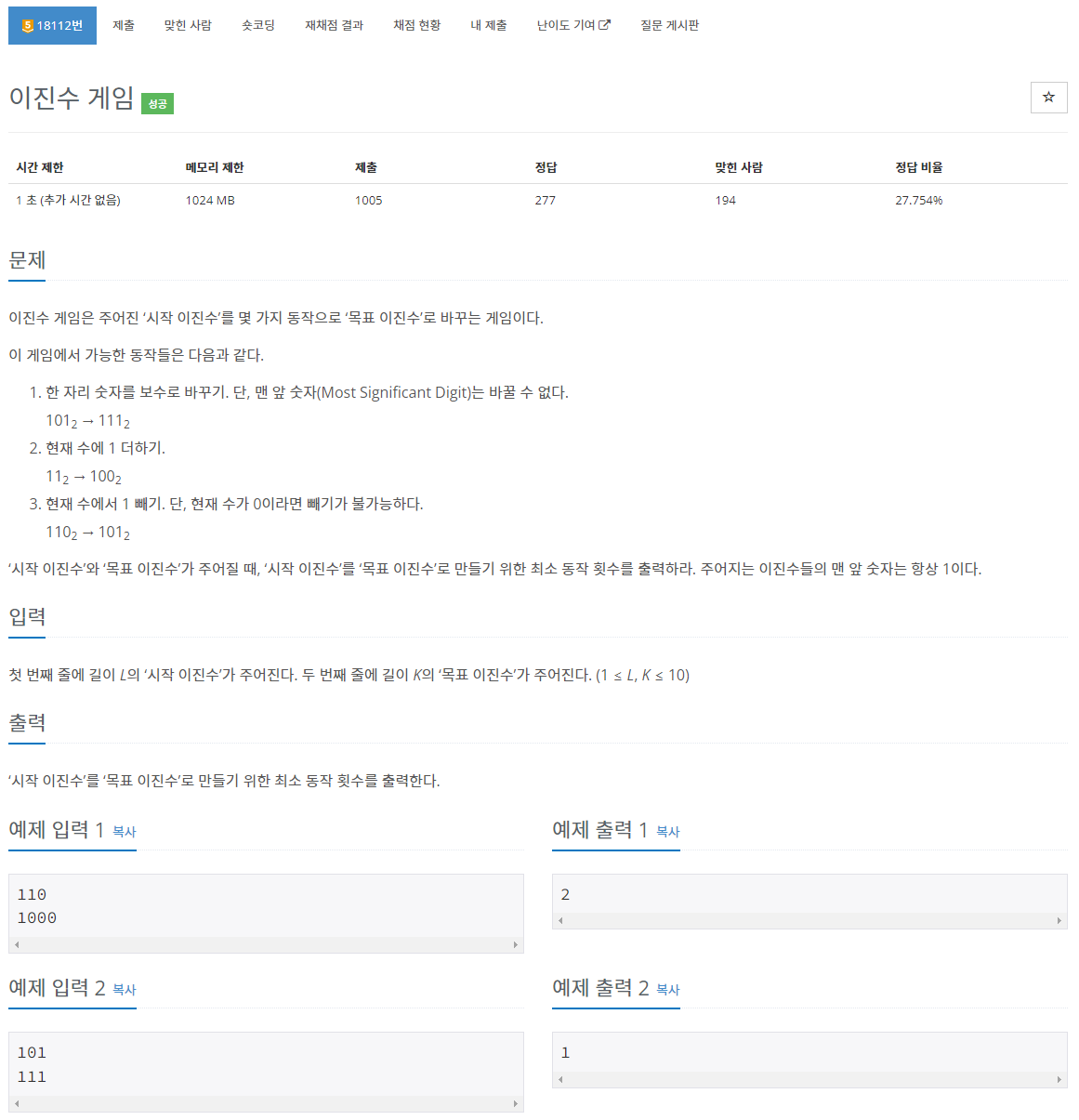
문제 : boj18112
필요 알고리즘
- BFS (너비우선탐색)
- 시작 이진수부터 목표 이진수까지 문제에서 제시된 동작들을 통해 순회하며 BFS를 진행하는 문제이다.
- 비트마스킹
- 애초에 문제 자체가 비트연산을 사용하는걸 전제로 만들어진 듯 하다. 안 쓸 이유가 없다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
BFS를 모른다면 'BFS 알고리즘 (너비 우선 탐색)' 글을 먼저 읽어보자.
이 글에 제시된 동작들은 모두 비트연산으로 수행 시 편하게 되어 있다. 그러니 우선 입력받은 시작 이진수와 목표 이진수를 2진수로 입력받자. 자바에서는 Integer.parseInt의 두 번째 인자로 radix를 넣어줄 수 있다. 예를들어 '110'을 아래처럼 입력받으면 10진수 6이 변수에 담긴다. 이하 시작 이진수는 'S', 목표 이진수는 'E'라고 하겠다.
int s = Integer.parseInt(br.readLine(), 2);
int e = Integer.parseInt(br.readLine(), 2);
동작 2번과 3번은 각각 +1, -1로 단순히 s++, s-- 로 수행 가능하므로 문제가 안될 것 같다. 동작 1번이 어려울 수 있다. 우선 맨 앞 숫자(가장 좌측에 나온 '1' 비트의 위치)를 알아야 한다. 직접 구해줘도 되지만 자바에서 'highestOneBit' 함수를 쓰면 얻어진다. 예를들어 10진수 7은 2진수로 '111' 이다. highestOneBit의 결과는 가장 좌측 '1' 비트만 남긴 수로, 2진수로 '100'가 나온다. 즉, 10진수 '4'가 결과로 나온다. 이를 이용하면 문제에서 설명한 'Most Significant Digit' 까지 반복문을 돌릴 수 있다. 그리고 각 비트를 보수로 바꾸는건 'bitwise exclusive OR' 연산 ('^')으로 가능하다.
이하 코드에서 getNextCandidates()가 이 문제에서 제시된 동작들을 통해 다음 이동할 위치 후보들을 구하는 함수이다.
private List<Integer> getNextCadidates(int n) {
List<Integer> candidates = new ArrayList<>();
if (n+1 < LIMIT) candidates.add(n+1); // 동작2
if (n != 0) {
candidates.add(n-1); // 동작3
int bit = 0; // 이하 동작1
int msd = Integer.highestOneBit(n); // 위에서 설명한대로 Most Significant Digit 획득
while ((1<<bit) != msd) { // msd까지 반복문 진행
int tmp = n^1<<bit++; // bitwise exclusive OR로 각 비트에 보수를 취한 값 획득
if (tmp < LIMIT) candidates.add(tmp);
}
}
return candidates;
}
그리고 다음 이동할 후보들만 제대로 얻었다면 나머지는 일반적인 BFS로 풀 수 있다.
while (!q.isEmpty()) {
int[] cur = q.poll();
if (cur[0] == e) {
System.out.println(cur[1]);
return;
}
for (int next : getNextCadidates(cur[0])) {
if (v[next]) continue;
v[next] = true;
q.add(new int[] {next, cur[1]+1});
}
}
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
private static final BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 1<<16);
private static final int LIMIT = 1<<10;
public static void main(String[] args) throws Exception {
new Main().solution();
}
public void solution() throws Exception {
int s = Integer.parseInt(br.readLine(), 2);
int e = Integer.parseInt(br.readLine(), 2);
if (s==e) {
System.out.println(0);
return;
}
boolean[] v = new boolean[LIMIT];
Queue<int[]> q = new ArrayDeque<>();
v[s] = true;
q.add(new int[] {s, 0});
while (!q.isEmpty()) {
int[] cur = q.poll();
if (cur[0] == e) {
System.out.println(cur[1]);
return;
}
for (int next : getNextCadidates(cur[0])) {
if (v[next]) continue;
v[next] = true;
q.add(new int[] {next, cur[1]+1});
}
}
}
private List<Integer> getNextCadidates(int n) {
List<Integer> candidates = new ArrayList<>();
if (n+1 < LIMIT) candidates.add(n+1);
if (n != 0) {
candidates.add(n-1);
int bit = 0;
int msd = Integer.highestOneBit(n);
while ((1<<bit) != msd) {
int tmp = n^1<<bit++;
if (tmp < LIMIT) candidates.add(tmp);
}
}
return candidates;
}
}
'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 1326 - 폴짝폴짝 (java) (0) | 2023.03.09 |
|---|---|
| [자바] 백준 1251 - 단어 나누기 (java) (0) | 2023.03.08 |
| [자바] 백준 13015 - 별 찍기 - 23 (java) (0) | 2023.03.07 |
| [자바] 백준 1194 - 달이 차오른다, 가자. (java) (0) | 2023.03.06 |
| [자바] 백준 18513 - 샘터 (java) (2) | 2023.03.03 |





댓글