문제 : boj20303

필요 알고리즘 개념
- 분리집합 또는 dfs 또는 bfs
- DP로 실제 답을 구하는 로직 이전에 아이들의 그룹을 만들기 위해 분리집합 알고리즘(union-find) 혹은 그래프 탐색이 필요하다. 이하 풀이는 분리집합으로 풀었다.
- DP (Knapsack)
- DP 활용법 중 유명한 냅색류의 문제이다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
결국 연결된 아이들의 그룹별로 선택할 수 밖에 없다. 따라서 만약 각 아이들 그룹별 아이들의 수와 해당 그룹의 아이들이 가지고 있는 사탕의 총합을 그룹별로 안다고 해보자. 이건 dfs, bfs 혹은 풀이 맨 아래에 포함된 코드처럼 분리 집합 알고리즘으로 구해주면 된다. 예를들어 예제 입력 1에 대해 전처리된 데이터는 아래와 같다.

이 데이터 중 필요한건 그룹당 아이의 수와 사탕 총합이다. 위와 같이 전처리를 한 후에는 K 미만의 아이 수를 포함하는 최대 사탕 총합의 합을 구해주면 된다. 이 경우는 냅색을 사용해서 풀어주면 된다. 그룹 번호 순서대로 냅색을 진행해보면 아래와 같이 구해진다. K=6 이므로 dp[5]로 두고 냅색을 진행하는 것이다.
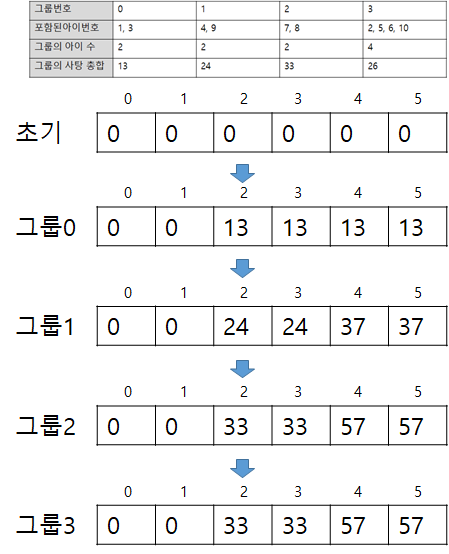
최종적으로 dp[k-1] = 57이 답이 된다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;
public class Main {
private static final BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 1<<13);
int[][] parents;
public static void main(String[] args) throws Exception {
new Main().solution();
}
private int find(int a) {
if (parents[0][a] < 0) return a;
return parents[0][a] = find(parents[0][a]);
}
private int findCandy(int a) {
a = find(a);
return parents[1][a];
}
private void union(int a, int b) {
a = find(a);
b = find(b);
if (a==b) return;
int hi = parents[0][a]<parents[0][b] ? a:b;
int lo = parents[0][a]<parents[0][b] ? b:a;
parents[0][hi] += parents[0][lo];
parents[1][hi] += parents[1][lo];
parents[0][lo] = hi;
}
public void solution() throws Exception {
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
int k = Integer.parseInt(st.nextToken());
parents = new int[2][n+1];
Arrays.fill(parents[0], -1);
st = new StringTokenizer(br.readLine());
for (int i = 1; i <= n; i++) {
parents[1][i] = Integer.parseInt(st.nextToken());
}
List<Integer>[] edges = new ArrayList[n+1];
for (int i = 1; i <= n; i++) edges[i] = new ArrayList<>();
while (m-->0) {
st = new StringTokenizer(br.readLine());
union(Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken()));
}
List<int[]> group = new ArrayList<>();
for (int i = 1; i <= n; i++) {
if (i != find(i)) continue;
group.add(new int[]{-parents[0][i], parents[1][i]});
}
int[] dp = new int[k];
for (int[] each : group) {
int a = each[0];
int b = each[1];
for (int i = k-1; i >= a; i--) {
dp[i] = Math.max(dp[i], dp[i-a]+b);
}
}
System.out.println(dp[k-1]);
}
}'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 27157, 26081 - GGANALi, 곰곰이와 GGANALi (java) (2) | 2023.01.13 |
|---|---|
| [자바] 백준 21740 - 도도의 수학놀이 (java) (0) | 2023.01.11 |
| [자바] 백준 8783 - Architektura niezależna (java) (0) | 2023.01.10 |
| [자바] 백준 2571 - 색종이 - 3 (java) (0) | 2023.01.10 |
| [자바] 백준 11663 - 선분 위의 점 (java) (0) | 2023.01.09 |





댓글