문제 : boj2571

필요 알고리즘 개념
- 누적 합 (prefix sum)
- 2차원 누적합 문제인데, 빈 공간을 포함하지 않기 위한 아이디어가 필요하다.
※ 제 코드에서 왜 main 함수에 로직을 직접 작성하지 않았는지, 왜 Scanner를 쓰지 않고 BufferedReader를 사용했는지 등에 대해서는 '자바로 백준 풀 때의 팁 및 주의점' 글을 참고해주세요. 백준을 자바로 풀어보려고 시작하시는 분이나, 백준에서 자바로 풀 때의 팁을 원하시는 분들도 보시는걸 추천드립니다.
풀이
내 경우 누적합 알고리즘으로 O(N^4)으로 풀었다. 다만 실제로 N^4은 아니고, 약간의 백트래킹도 포함되었고, 한쪽 방향으로 탐색 범위를 고정했으므로 4중 반복문이긴 하지만 N^4보단 낮다.
우선 2차원 누적합 알고리즘으로 직사각형의 넓이를 O(1)로 획득 가능해야 한다. 이 부분은 '누적 합(prefix sum), 2차원 누적합(prefix sum of matrix) with java' 글의 '2차원 누적 합 (prefix sum of matrix)' 부분을 참고하자.
2차원 누적합으로 모든 범위의 넓이를 구해두고, 직사각형의 좌측 상단을 (x, y), 우측 하단을 (x2, y2)라 할 때 모든 x,y,x2,y2 쌍에 대해 직사각형의 넓이를 각 O(1)로 구해 그 중 가장 큰걸 출력해주면 된다. 다만 이어지는 구간을 골라야 하므로, 아래의 빨간 네모처럼 빈 공간을 포함해서 직사각형을 만들면 안된다.
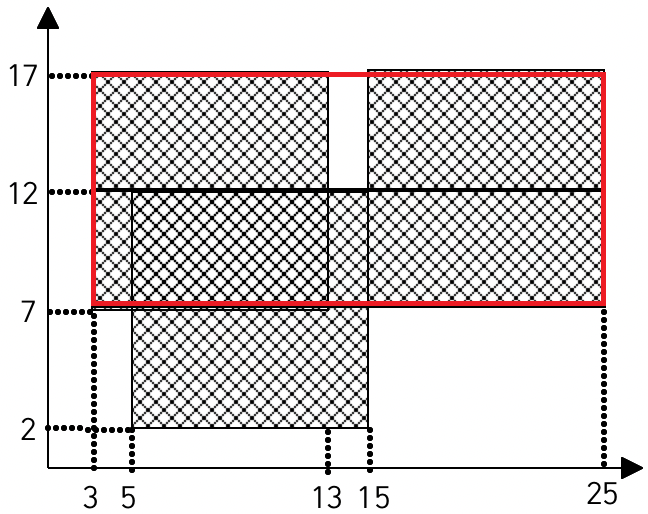
이 부분 처리에서 다소 어려울 수 있는데, 심플한 아이디어로 별다른 처리 없이 걸러낼 수 있다. 빈 공간을 '-무한대'로 설정하면 된다(여기서 무한대는 이 문제에서 나올 수 있는 최대 넓이보다만 크면 된다.). 그럼 빈 공간을 포함하는 직사각형 부분은 넓이가 항상 음수가 될 것이므로, 처음에 배열 초기화만 -무한대로 해주면 별다른 처리없이 걸러낼 수 있다.
코드 : github
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
private static final int SQUARE_LENGTH = 100;
private static final BufferedReader br = new BufferedReader(new InputStreamReader(System.in), 1<<13);
private static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws Exception {
new Main().solution();
}
public void solution() throws Exception {
int n = Integer.parseInt(br.readLine());
int[][] arr = new int[SQUARE_LENGTH+1][SQUARE_LENGTH+1];
for (int[] row : arr) // -무한대로 초기화
Arrays.fill(row, -10001);
while (n-->0) {
StringTokenizer st = new StringTokenizer(br.readLine());
int r = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
for (int i = r; i < r+10; i++) {
for (int j = c; j < c+10; j++) {
arr[i][j] = 1;
}
}
}
int[][] prefixSum = new int[SQUARE_LENGTH+1][SQUARE_LENGTH+1];
for (int i = 1; i <= SQUARE_LENGTH; i++) { // 2차원 prefix sum
for (int j = 1; j <= SQUARE_LENGTH; j++) {
prefixSum[i][j] = arr[i][j] + prefixSum[i-1][j] + prefixSum[i][j-1] - prefixSum[i-1][j-1];
}
}
int answer = 0;
for (int i = 1; i <= SQUARE_LENGTH; i++) {
for (int j = 1; j <= SQUARE_LENGTH; j++) { // (i,j)는 직사각형의 좌측 상단
for (int ib = i+1; ib <= SQUARE_LENGTH; ib++) {
for (int jb = j+1; jb <= SQUARE_LENGTH; jb++) { // (ib,jb)는 직사각형의 우측 하단
int area = prefixSum[ib][jb] - prefixSum[i-1][jb] - prefixSum[ib][j-1] + prefixSum[i-1][j-1];
if (area < 0) break; // j<jb이고 jb는 항상 증가하므로 한번이라도 음수라면 그 뒤로 전부 음수이므로 무시한다.
answer = Math.max(area, answer);
}
}
}
}
System.out.println(answer);
}
}'PS > BOJ' 카테고리의 다른 글
| [자바] 백준 20303 - 할로윈의 양아치 (java) (0) | 2023.01.11 |
|---|---|
| [자바] 백준 8783 - Architektura niezależna (java) (0) | 2023.01.10 |
| [자바] 백준 11663 - 선분 위의 점 (java) (0) | 2023.01.09 |
| [자바] 백준 14927 - 전구 끄기 (java) (0) | 2023.01.06 |
| [자바] 백준 9024 - 두 수의 합 (java) (0) | 2023.01.04 |





댓글